連続時間強化学習(中編)

Miyamoto

---

1 はじめに

今回は、予告通り連続時間強化学習の続きを解説します。非常に難易度が高くなってしまいました。前回難解なと言っていたPOMDPよりも遥かに上であると言えるでしょう。

確率解析の修士の学生のうち、ジャンプ過程にかかわる専門でない場合は、優秀層なら理解できるかな、というくらいの難易度になってしまいました。

まず、[1] では報酬のきちんとした定義が捨て置かれています。

一番楽なのは$r_t$も通常のガウス過程としてしまうことですが、それだとあまりにも強化学習の実応用において、実態を反映できていない理論になってしまうと考えました。

そのため、より、強化学習の報酬に近い挙動をする確率過程を考えることにしました。そうやって使うことにしたのが、今回取り扱う飛躍型確率微分方程式です。

実際、待ち行列理論などではポアソン分布が使われることからもわかる通り、ポアソン測度を用いた定式化は強化学習の実態に沿っていると言えるでしょう。

2 飛躍型確率微分方程式

ここではジャンプ過程について簡単に解説します。

2.1 Levy 過程とポアソンランダム測度

定義1 Levy 過程

確率過程\(\{ z_t \} \)が\(Levy\)過程であるとは、次の5 条件を満たすものを指す。

• \(z_0 = 0\)
• 任意の\(t, h > 0\)に対して、\(z_t\)と\(z(t + h) − z(t)\)は独立、独立増分性
• \(Law(z(t + h) − z(t)) f(h)\)、定常増分。つまり\(z(t + h) − z(t)\)は\(t, z(t)\)によらない
• 任意の\(\epsilon, t\)に対して\(\lim _{h\to 0+} P(|z(t + h) − z(t)| > \epsilon) = 0\)、確率連続性
• 右連続な経路を持ち、また左極限を持つ

さらに、ジャンプした場面を次のように書きます。

---

(1)

\[\Delta _z(t):=z(t)-z(t-)\]

---

\(|\Delta z(t)|>0\)になるような\(t\)が、ジャンプした瞬間です。

ここで、計数過程\(N(t, A)\)を次のように定義します。ただし、\(A \subset \mathbb{R} / 0\)です。

---

(2)

\[N(t, A):=\sum_{0 \leq s \leq t} 1_{A}(z(t))\]

---

つまり、\(A\)にはまるジャンプ幅を何回やったかカウントします。

次に、時刻区間\((a, b]\)の値を次のように定義します。

---

(3)

\[N((a, b], A)):=N(b, A)-N(a, A)\]

---

定義から明らかなように、\(N\)は、測度のような集合関数でありながら、その値はランダムです。そのため、ランダム測度と呼ばれます。

ここで\(Levy\)測度\(\mu\)を次のように定義します。

---

(4)

\[\mu(A):=E[N(1, A)]\]

---

つまり、1 単位の時間幅で、\(A\)の範囲のジャンプを行う回数の期待値です。

\(Levy\)測度を用いて\(N(T × A)\)が指数\(\mu(T × A)\)のポアソン分布になり、さらに互いに祖な集合に対し確率変数として\(N\)同士が独立なとき、これをポアソンランダム測度と言います。

さらに\(Levy\)測度は次の性質を満たすとします。

---

(5)

\[\int_{\mathbb{R} / 0} \min \left(1,|z|^{2}\right) d \mu(z)<\infty\]

---

ここで、次の式が成り立つとすると\(^{\ast 1}\)

---

(6)

\[\int_{|z| \geq 1}|z| d \mu(z)<\infty\]

---

\(z(t)\)は次のように書き換えられます。

---

(7)

\[\int_{0}^{t} \int_{\mathbb{R} / 0} \gamma^{s} z \tilde{N}^{\pi}(d s, d z)+\frac{\gamma^{t}-1}{\log \gamma} \int_{|z|>1} z \mu(d z)\]

---

ただし、これは後述の\(R\)の定義に沿っていることに注意。強化学習であるため、\(γ^s\)という減衰項がついています。

この積分は、ポアソンランダム測度に対する確率積分です。詳細は[2][3] などを参照。

一つ重要な性質として

---

(8)

\[E\left[\int_{0}^{t} \int_{\mathbb{R} / 0} \gamma^{s} z \tilde{N}^{\pi}(d s, d z)\right]=0\]

が成り立ちます。

---

\( ^{\ast 1} \)ダイナミックプライシングをはじめとする強化学習で用いる場面でこれが成り立たない状況は違和感があるので、強化学習の理論としてはこれも仮定していいかもしれません。

2.2 伊藤の公式

このような\(Levy\)過程\(z_t\)に対しても伊藤の公式を考えることができます。

定理1 伊藤の公式

確率過程\(X_t\)が次の飛躍型確率微分方程式を満たすとします。

---

(9)

\[X_{t}:=/ * \int_{0}^{t} \int_{\mathbb{R} / 0} \gamma(z) \tilde{N}(d s d z)\]

---

ただし、\(c\)は定数で\(\gamma\)は\(\int_{\mathbb{R} / 0} \gamma(z)^{2} d \mu(z)<\infty\)とします。

ここで、\(C^2\)級関数\(f\)を用いて、\(Y_t = f(X_t)\)とすると、

---

---

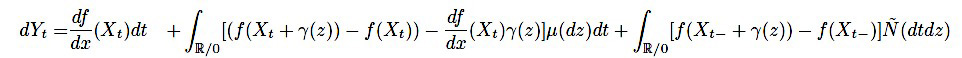
が成り立ちます。

2.3 状態依存型ジャンプ過程

ここまでは、ジャンプの頻度や飛び方が今の状態に関係ないものと考えてきました。

しかし実際の強化学習を考えてみると、そんなわけはありません。

これについては現在研究中です。[4] の定義ではちょっと曖昧過ぎるので、定義からやり直していろんな証明をしています。あとがきで少々語る予定。

3 定義とベルマン方程式

3.1 累積報酬和

報酬を\(R_t\)と書き、これを「累積報酬」と定義します。累積報酬は\(Levy\)過程で、次の飛躍型確率微分方程式に従っているものとします。

---

(10)

---

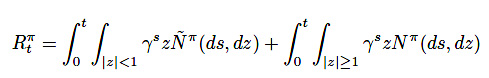
\(\gamma\)は一般の強化学習でもよく出てくる、割引報酬率の\(\gamma\)です。

通常の複合ポアソン過程などでは、この計上を自然な形で行うことができないため、こうして飛躍型確率微分方程式を用いたほうが(数学的な難易度は劇的に上がるのと引き換えに)圧倒的に見通しがよくなります。

さらに、今回はダイナミックプライシングというタスクで考えている関係上、\(A:={x \in \mathbb{R}: x<0}\)と定義すると\(N(t,A) = 0\)であるものとします。つまり上にしかジャンプしません。\(^{\ast 3}\)

この\(x_t,a_t,R_t\)の族を、「飛躍型連続時間マルコフ決定過程」と呼ぶことにします。

---

\( ^{\ast 2} \)ここの定義が一番難しかった。

\( ^{\ast 3} \)他のタスクでは、必要であれば\(R_t\)や\(N\)の性質を少し変更することで、ガウシアンノイズを加えたり、定常的なコストを考慮することもできます。今回は初回でかつダイナミックプライシングを見据えた記事ということで、このような定義を採用しました。

4 ハミルトン・ヤコビ・ベルマン方程式

ここでは、確率制御で重要になるハミルトンヤコビベルマン方程式について解説します。

ベルマン方程式ごときではもはや対処できない代物です。ハミルトンヤコビベルマン方程式に頼りましょう。

これは本来は時空の偏微分方程式ですが、後述の強化学習特有の工夫により空間のみの偏微分方程式になります。

今回はモデルベース型となります。すなわち、計数を推定して行います。

単純化のため、次のような確率微分方程式を想定します。

---

(11)

\[d X_{t}=b\left(t, X_{t}, u_{t}\right) d t+\sigma\left(t, X_{t}, u_{t}\right) d B_{t}\]

ただし、\(u_t\)は取る行動です、

また、評価関数は次のように定義されるとします。

---

(12)

$$\max {u} \int{0}^{T} C\left(t, X_{t}, u_{t}\right) d t+D\left(X_{T}\right)$$

---

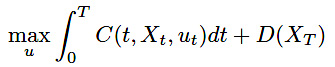
これに対して、次の定理が成り立ちます。

定理2 ハミルトンヤコビベルマン方程式

最適状態価値関数\(V(t, x)\)は次の偏微分方程式に従う。

---

(13)

---

(14)

\[V(T, x)=D(x)\]

---

ただし、\(A^u\)は伊藤拡散過程の生成作用素であり\(f \in C^{1,2}\left(\mathbb{R}, \mathbb{R}^{d}\right)\)に対して(\^{ast4})

---

(15)

---

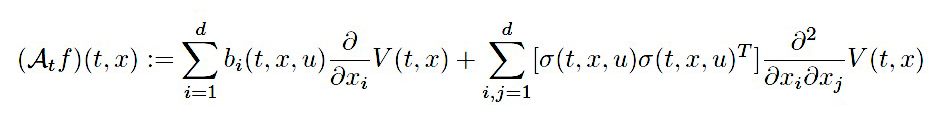
\(T\)は転置行列の意味です。

これは生成作用素と言います。本来上記式は定義ではなく定理であり、厳密な定義としては確率過程\(X_t\)に対して

---

(16)

---

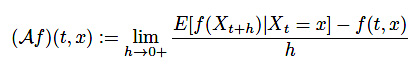
と定義されます。
proof.

ハミルトンヤコビベルマン方程式の導出の証明をします。
まず、ベルマン原理により\(h > 0\)に対して

---

(17)

---

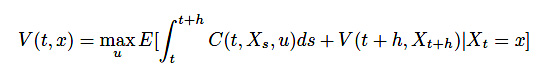
が成り立ちます。右辺を変形していきましょう。

---

---

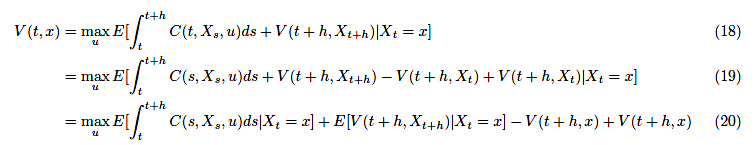
最後の項を左辺に移して、両辺を\(h > 0\)で割ります。

(21)

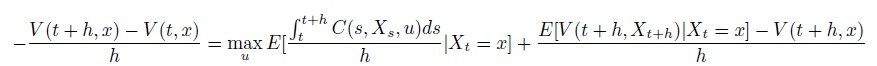
ここで、両辺を\(h \to 0 \)とすると、これは上からの収束なので

---

(22)

\[-\frac{\partial}{\partial t} V(t, x)=\max _{u}\left[\mathcal{A}^{u} V(t, x)+C(t, x, u)\right]\]

となって、ハミルトンヤコビベルマン方程式が導出できました。

あとでこの導出をほんのひとひねりすることで、強化学習のようなポアソン報酬型に対してもハミルトンヤコビベルマン方程式を考えることができるようになります。\( ^{\ast 5} \)

見ての通りハミルトンヤコビベルマン方程式は非線形の偏微分方程式です。それも2 乗や\(log\)などの単純なものではなく、\(max\)という非常に厄介な項がついています。

当然古典解\( ^{\ast 6} \)を解析的に求めるのは不可能に近く、粘性解という申し開きすら盛んにおこなわれていたりします。

---

\( ^{\ast 4} \)時間に対してC1級、空間に対してC2級

\( ^{\ast 5} \)ここが弊社の新発見！詳細は論文投稿後掲載する後編にて

\( ^{\ast 6} \)普通の関数の形でかける解

4.1 粘性解

上述の通り、ハミルトンヤコビベルマン方程式は古典解を求めるのが非常に困難です。

粘性解の概念について、簡単に解説します。

定義2 粘性解

任意の\(x \in X \subset \mathbb{R} ^d\)で定義された\(H(x,u,Du,D^2u) = 0\)という偏微分方程式が退化楕円型であるとは、任意の正定値行列\(Y – X\)に対して、任意の\(x,y,p \mathbb{R}に対して\)

---

(23)

\[H(x, y, p, Y) \geq H(x, y, p, X)\]

---

が成り立つものをいいます。連続性については仮定すると、次の粘性劣解、粘性優解が定義できます。

任意の点\(x_0 \in X\)に対して、ある\(x_0\)の近傍\(A\)が存在し、\(\phi\left(x_{0}\right) \geq u\left(x_{0}\right)\)で任意の\(x \in A\)に対して\(\phi(x) \geq u(x)\)が成り立つような任意の\(C^2\)級関数\(\phi\)に対して、\(H\left(x_{0}, \phi\left(x_{0}\right), D \phi\left(x_{0}\right), D^{2} \phi\left(x_{0}\right)\right) \leq 0\)が成り立つとき、\(u\)を粘性劣解という。

任意の点\(x_0 \in X\)に対して、ある\(x_0\)の近傍\(A\)が存在し、\(\phi\left(x_{0}\right) \geq u\left(x_{0}\right)\)で任意の\(x \in A\)に対して\(\phi(x) \leq u(x)\)が成り立つような任意の\(C^2\)級関数\(\phi\)に対して、\(H\left(x_{0}, \phi\left(x_{0}\right), D \phi\left(x_{0}\right), D^{2} \phi\left(x_{0}\right)\right) \geq 0\)が成り立つとき、\(u\)を粘性優解という。

\(u\)が粘性優解かつ粘性劣解であるとき、これを粘性解と言う。

これは、一意性、存在性、安定性の3 つの重要な指標があります。詳細は省略しますが、安定性とは粘性解の列が\(L \infty \)の意味でなにかしらの粘性解に収束することを言います。

5 今後の課題

5.1 状態依存型ポアソンランダム測度について

私がここ数か月尽力している連続時間強化学習の研究は、ほぼこの非定常なポアソンランダム測度と、それによる確率積分・伊藤の公式などの研究に費やされました。\(^{\ast 7}\)

ここさえ乗り切ってしまえばあとはほぼ既存の確率制御の研究でなんとかなるので、本研究の本丸ともいえるでしょう。

一応、一切この研究がないわけではないのですが、強化学習には使えない限定的な状況であったり、[4] のように厳密性に欠けるものしかみあたらず、厳密な基礎理論を弊社で内製することにしました。

現状、9 割がた初期理論としては出来上がってきています。全て論文公開前なので、ここには書けません。

応用数学のジャーナルに投稿予定ですが、その前段階としてarXiv に書いた段階でお知らせや中身の解説はできるかと思われます。\(^{\ast 8}\)

ここ50 年ほどは、この立場に物理学以外に経済学も算入してきました。特に数理ファイナンスは、近年確率解析分野における数学との相互発展が著しいです。

一方で、機械学習はまだこの立場になっていません。

数学を機械学習に用いることはあれど、機械学習に必要だからという理由での数学の研究は、情報幾何等の特殊分野を除いて存じ上げません。

この強化学習での必要性に迫られたことによる確率解析の新展開（というのは大げさかもしれませんが）は、機械学習と数学の相互発展の歴史の第一歩となるかもしれません。

---

\( ^{\ast 7} \)この研究を通して、ただ難しくて読みにくいだけだと思っていた[7] のすばらしさを思い知らされました。

\( ^{\ast 8} \)有名なのはフーリエ解析、デルタ関数。実は三角関数なども当てはまります。

5.2 分布型強化学習の導入とエルゴード性

論文[1] では最尤法などで定式化が行われ、漸近正規性などの考察が行われていますが、ここはやはり通常の強化学習に倣って、ベルマン作用素で最適化していくべきだと思われます。

また、分布型にすることで、エルゴード性の議論に持ち込むことができ、より楽に解析することができることが期待されます。

参考文献

[1] Tianhao Chen, Limei Cheng, Yang Liu, Wenchuan Jia and Shugen Ma, Fellow, Incremental Reinforcement
Learning a New,Continuous Reinforcement Learning Frame Based on Stochastic Differential Equation
methods , IEEE 2018
[2] 石川保志, ジャンプ型確率過程とその応用, 琉球大学講義ノート,2014
[3] Makiko Nisio,Stochastic Control theory-Dynamic programming principle,springer,2015
[4] Floyd B. Hanson,Applied Stochastic Processes and Control for Jump Diffusions: Modeling, Analysis, and
Computation,2007
[5] Mark Rowland,Marc G.Bellemare,Will Dabney,Remi Munos,Yee Whye Teh,An Analysis of Categorical
Distributional Reinforcement Learning,arxiv:1802.08163,2018
[6] A. Yu. Veretennikov , On polynomial mixingbounds for stochastic differential equations. Stochastic Process.
Appl. 70, 115–127.1997
[7] P. Protter, Stochastic Integration and Differential Equations, 2nd ed., Stoch. Model. Appl. Probab., Vol.
21, Springer, Berlin, Heidelberg, 2005.