Miyamoto
1 はじめに
参考資料は「一般化線形モデルによる価格弾力性推定に基づく粗利最大化」関 庸一, 亀倉 大和 2012である。
我々は強化学習を用いた最適な値付け戦略について、研究開発を日々行っているが、価格弾力性を考慮すればよりよいアルゴリズムが作ることができると考えられる。
2 前提
価格弾力性の基礎的な説明は(下記の記事)参照
●ミクロ経済学の基礎~弾力性- \(d: \) 日付
- \( s: \) 店舗
- \( P: \) 価格
- \( A: \) 売り上げ
- \( \xi: \) 価格弾力性
- \(\hat{x} : \) 未知定数 \(x\) の推定量
- \( p_{ds}: \) 日付\(d\)における店舗\(s\)での売り上げ
- \( \tilde{p}: \) その商品の平均価格
- \( z_{sd}: \) 掛率。\(z_{sd} = p_{sd} / \tilde{p} \) で計算される。
- \( z_{max}: \) 掛率ベースで定義された値段の上限 \( ^{\ast 1} \)
- \( c: \) 仕入れ値の掛率
- \( Po:\)ポアソン分布
3 基礎知識
売り上げを価格の関数として\(A(p)\) と置く。
考えうる価格帯で価格弾力性は一定であると仮定すると。
(1)
\[\frac{d A(p)}{d p}=-\xi \frac{A(p)}{p}\]
この常微分方程式を解くと
(2)
\[A(p)=C p^{-\xi}\]
ただし\(C\)は積分定数である。これが需要曲線であると考える。\( ^{\ast 2}\)
掛率は上記の定義とする。原価割れでの販売は考慮しない3ものとし、掛率は\(0 < c \leq z_{sd} \leq z_{max}\)が成り立つとする。
3.1 一般化線形モデル
\(s; d\)に対する線形予測子\(\eta_{s d}:=\log \left(E\left[A_{s d}\right]\right)\)を
- \( ^{\ast 1} \)我が社の案件でも、ほとんどの場合この上限や下限の設定がある。これを「考えうる価格帯」と呼ぶものとする
- \( ^{\ast 2} \) 「価格弾力性が一定」と言うと\(dA(p)/dp\) が定数であるかのように錯覚しがちだが、これは誤りである。注意されたし。
- \( ^{\ast 3} \) 実際には破棄コストや回収率を考えた場合、多少仕入れ値を割ってでも売り切ったほうが良いこともある。スーパーで夜になると半額になったりするアレだ。特に食品にありがち。今回は考慮しない。
(3)
となっているものとする。ただし、\(x_{sdj} \)は店舗と日付ごとの説明変数、\( \beta_j\) はその係数であるものとする。
\(- \beta _{1s}\)は、店舗\(s\)における価格弾力性である。\(^{\ast4}\)
4 利益最大化
粗利益の期待値\(g_{sd}\)は
(4)
(5)
\(C_{sd}\)は店舗と日付ごとの定数である。
ここで重要なのは、\(\eta\)の定義において、たくさんの説明変数や係数が登場した。それらの相関の考慮や、なにより全体の数やスケールといった多くの難題が、期待値の考察においては\(C_sd\)という一つの定数に集約できるという点。
これによって無関係な定数倍である \(C_sd\)を考慮せずとも最大化の考察ができるので、戦略の導出には「価格弾力性と平均価格、仕入れ値さえあれば良い」ということがわかる。
というわけで、次の関数を最大化する\(z\)を求める。
(6)
\[g(z):=\tilde{p}(z-c) z^{-\xi}\]
\(z^\ast := argmax_zg(z) \)は、自明に上の期待粗利を最大化するz と等しい。\(^{\ast 5 }\)
ここで、\(0 < c \leq z \leq z_{max}\)という制約条件があるため、前回同様\(\xi > 0\)であることに注意して
(7)
\[g^{\prime}(z)= \tilde{p} \left(z^{-\xi}+(z-c)(-\xi) z^{-(\xi+1)}\right)\]
ここで、\(g′(z) = 0\)となるとき、\(z = \frac{c\xi}{\xi-1} \)のみである。\(\xi= 1\) のとき極値は存在しない。この\(z\)が\([c; z_{max}]\) に収ま り、かつ二階導関数が負なら、これが\(z^\ast\)である。
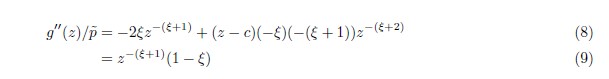
最後の変形は \(z = \frac{c\xi}{\xi-1} \) を代入した。\( \tilde{p}, z > 0\)であるため、\(\xi> 1\) ならこれは極大値、\(\xi < 1\)ならこれは極小値である。
しかし \(\xi,c > 0\)であるため \(\frac{c \xi}{\xi-1} \in\left[c, z_{m a x}\right]\) となる必要条件は \(\xi> 1\) である。
よって、 \(\frac{c \xi}{\xi-1} \in\left[c, z_{m a x}\right]\) なら
\(z = \frac{c\xi}{\xi-1} \)
\(\xi \leq 1\) もしくは \(\xi> 1\) であっても\(\frac{c \xi}{\xi-1} \notin\left[c, z_{m a x}\right]\)であるとき、\(g'(z) = 0 \)となる\(z \in [c,z_{max}]\)は存在しないので、\( [c,z_{max}] \)において、単調減少か単調増加のどちらかである。
よって、\(z = c,z =_{max} \)の場合を比較すればよい。
(10)
\[g(c) = 0\]
(11)
\[g(z_{max}) > 0\]
以上より、次が成り立つ
- \(^{\ast 4 }\) 実際、地域などの要因によって、価格弾力性は変化して当然である。
- \(^{\ast 5 }\) 期待粗利最大化戦略を求めるときは、\(C_{sd}\)を推定する必要すらないのである。具体的な期待粗利は不明でも、それが最大化戦略であることはわかるためである。
(12)
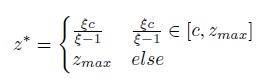
後者の場合、価格弾力性が一定である区間では、際限なく価格を上げるのが正解ということになる。
ここから、上限で売ることを「定価政策」と呼び、解析的に求まった\(\frac{\xi c}{\xi -1}\)で売ることを「特価政策」と呼ぶ。
前回の記事では、\(\xi \leq 1\) は贅沢品、それ以外を必需品と呼んでいた。
4.1 短期政戦略と長期戦略
つまり、必需品は定価政策がよく、贅沢品の一部は特価政策がよいという結論になる。
贅沢品の内訳は、1 からの離れ具合が仕入れ値と最大値の差を埋めるような贅沢度(造語) が小さいものは定価政策で、贅沢度が大きいものは特価政策となる。
では、長期的にはどうか。
これを考察するにあたって、論文では「短期のみの仮定」として、次のような仮定がおかれている。
- 販売規模一定
- 考えうる価格帯において、弾力性は一定
- 仕入れ値率は一定
- 上限掛率は一定
長期的にはこれらの仮定はいずれも成り立たない場合があるものとする。
4.1.1 短期戦略
価格弾力性\(\xi\)を先述の一般化線形モデルにより推定。特価戦略か定価戦略かを決定する。
4.1.2 長期戦略
長期的には需要はより弾力的になりやすいらしい。代替効果も大きくなりがちだろう。短期粗利を減らしてでも、プロモーションなどを使って有利な価格弾力性への誘導が重要となる。
仕入れ値率を低くできた場合、定価政策から特価政策への移行が俎上に上がる場合がある。そのとき、最適掛率よりも低い値で販売プロモーションを行って価格弾力性を高くするのがよいとされている。
高くなってしまった場合、特価政策であれば最適掛率より高い掛率で売り続けて弾力性定価を狙い、定価政策への移行も検討する。
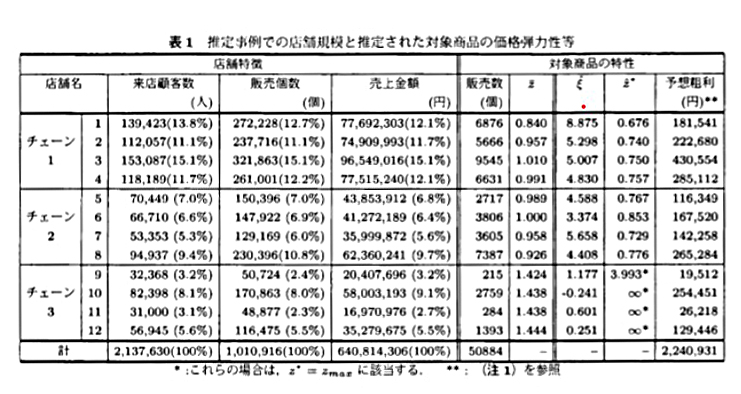
5 分析結果(引用)
この論文ではドラッグストアチェーン3つのそれぞれ4 店舗に対して解析を行っている。
(論文からの引用)
予想粗利は\(c = 0:6\)とおいた場合の試算である。
6 発展
価格弾力性の推定方法の一案として、需要予測関数をニューラルネットを用いて作成し、そこから微分と入出力の算出により価格弾力性を推定する方法が考えられる。
既存の価格弾力性推定データを活用する方法も考えられ、今後検証を行っていきたい。詳細は次回の価格弾力性記事第三弾で、できることなら結果とともに発表したい。
