ミクロ経済学の基礎~弾力性 - ダイナミックプライシングテクノロジー developers lab

Miyamoto

コンテンツ

1 はじめに

ダイナミックプライシングにおいては、価格弾力性を考慮したアルゴリズムの開発が課題となっている。

現状は強化学習などをもちいて、裏で勝手に考慮して最適化している（ことになっている）が、実際に組み込んでしまうことで、より性能の高い学習ができるようになることが期待される。

今回は主に[1] を参照した。画像も引用している。

この記事では、この価格弾力性や市場均衡の概念について、簡単に解説を行う。

参考文献
[1] 新版ミクロ経済学, 武隈真一,新世社,2016

2 基礎知識

商品が二つの市場を考える。

消費者の需要量を表す関数を$D_1 ,D_2$、それぞれの値段を$p_1,p_2$、所得を$m$とする。
$D_1 ,D_2$、は、どちらも$p_1,p_2,m$の関数である。

定義1 $0$次同時性

関数$D_1 ,D_2 : \mathbb{R}^3 \rightarrow \mathbb{R}$が次の条件を満たすとき、$0$次同時性を満たすと言う。

任意の$t > 0$に対し、

(1)

\[ D_1(p_1,p_2,m) = D_1(t_{p1,}t_{p2,}t_m) \]

(2)

$D_2(p_1,p_2,m) = D_1 (tp_{1,} t_{p2,} t_m) $

需要関数はこの0次同時性を満たすとする。

これは、経済学的な仮定の数式への落とし込みである。実際、値段と所得が同時に2倍になっても、購入できる量もそれに伴う満足度（経済学では効用という）も変わらない。

2.1 弾力性

現時点での需要数を$x_i := D_i$で表記するものとする。

需要の弾力性は、数学的には次のように定義される。

2.1.1 需要の所得弾力性

所得の微小な変化に対してどの程度需要が変化するかの指標である。

(3)

$\Delta m \rightarrow D$ として偏微分の形で書くと

\[ \eta _i := \frac{m}{x_i}\frac{\Delta D_i}{\Delta m}(p_1,p_2,m) \]

2.1.2 需要の価格弾力性

ダイナミックプライシングにおいて重要なのはこちらである。

$p_j$の微小変化に伴いどの程度$D_i$が変化するかの指標。

(4)

$\Delta P_j \rightarrow o$ として偏微分の形で書くと

\[ \epsilon _{ij} := – \frac{p_j}{x_i} \frac{\Delta D_i}{\Delta p_j}(p_1,p_2,m) \]

2.2 財の種別

ここで、個人ごとの需要関数を$D^u$と書く。$^{\ast 1}$

価格弾力性の議論は、その商品（以下、財）の性質や、他の製品に大きく影響を受ける。

2.2.1 必需品と下級財

ダイナミックプライシングとはあまり関係ないが、ミクロ経済学における基礎的知識なので紹介しておく。

おいしくて高い米とまずくて安い米の二財がある市場を考える。

消費者の収入が増えれば、我慢して食べている安い米をやめて、高くておいしい米を買うようになる。

つまり高い米は「収入が増えると需要が増える」、安い米は「収入が増えると需要が減る」ということになる。

こういった状況で、高い米を上級財、安い米を下級財という。

次に、収入が増減したとき、消費量が大きく変わるものが何かを考えたい。

主食や必須の日用品などは、収入が減ったところであまり減らせない。一方で、レジャー費用や高級品など、減らすことが可能であるものから大きく減らしていくのが普通である。

逆に、収入が増えたときこういったものの消費は大きく増える。日用品の消費量は、「節約しなくてもいい」ということで少しは増えるであろうが、さほど変わらない。

このように、収入変化による需要の変化が大きいものを「贅沢品」、少ないものを「必需品」と呼ぶ。厳密な定義は、上で述べた$\eta$が1 を上回ると贅沢品、下回ると必需品である。$^{\ast 2}$

これらとは別にギッフェン財と非ギッフェン財という区分も存在するが、これについて具体例を扱わない理由は後述。

以上の単語の定義を数式で書くと次のようになる。

$\eta_i > 1$の時、この財を贅沢品、それ以外の時を必需品と呼ぶ。
$\partial D_i/\partial m > 0$のとき、この財を上級財、それ以外を下級財と呼ぶ。
$\partial D_i/\partial p_i > 0$の時この財をギッフェン財であると呼ぶ。

この区分で、財は四種類に分類される。

贅沢品で上級財で非ギッフェン財
必需品で上級財で非ギッフェン財
必需品で下級財で非ギッフェン財
必需品で下級財でギッフェン財

価格を固定し、勾配を近傍のみで考えた場合これ以外の財が存在しえないことの確認は容易である。$^{\ast 3}$

値上がりによる実質的な所得減少（所得効果）が値上がりしても他所の商品に逃げたがる指向（代替効果）を大きく上回る極端な性質を持つ財がギッフェン財である。$^{\ast 4}$

2.2.2 補完財と代替財

焼肉用肉、パン、米の３つの財がある市場を考える。焼肉用肉の値段が下がり、焼肉ブームが起きたとする。焼肉と米は合う。これは大半の方が認めてくださる真理だろう。

家庭で焼肉を行うための食料品を買ったとき、家に米がない。そんなとき、米を我慢するだろうか。いや、そんなことはあり得ない。

$^{\ast 1}$実際には、個人の効用関数$u(x_1,x_2)$と予算制約線$p_1x_1+p_2x_2 = m$に対して値が定まる効用に対応した需要関数である。詳細はここでは解説しない。「個人単位の需要関数」という認識で十分である

$^{\ast 2}$明らかにわかる通り、現在の値段や需要、供給によって、必需品か贅沢品かは変わる。例えばマツタケが非常にわかりやすい例である。マツタケがなくても生きていけたから必需品ではないと思われるかもしれないが、辞書的な意味とは微妙に異なることに注意されたし。

$^{\ast 3}$ただし医薬品や健康食品の一部に、稀有な例外は存在するが、そもそも公理的に経済学の外にあるものである。

$^{\ast 4}$ギッフェン財なるものが実在するのかは定かではない。一説では、国と地域によってはジャガイモがギッフェン財なのではないかとされているが、本当のところは不明。実在するとすれば「仕方なく食べている安物の主食」であると言われている。

焼肉の値段が下がって焼肉が流行ると、当然米の需要も増える。これが「米が焼肉の補完財」という状況である。ではパンはどうか。焼肉が流行ると、パン食は下火になる。

もちろんジューシーな焼きたての肉を挟んだサンドウィッチは良いものだが、焼肉用の肉はそのような調理には向かない場合が多い。

つまり、焼肉はパンの代替財である。

そして米in パンは狂気の沙汰だ。稀には好む方もいるだろうが、間違いなく極めて少数派である。

よって米もパンの代替財になる。

「パンの値段が上がったから今年の食卓ないし給食は主に米」といった言葉やその逆は、一度は耳にしたことがあるだろう。

数式で書くと、次のようになる

(5)

\[ \frac{\partial D^u_i}{\partial p_j}<0 \rightarrow 補完財 \]

(6)

\[ \frac{\partial D^u_i}{\partial p_j}>0 \rightarrow 代替財 \]

これらの$D^u$を$D$に差し替えたものは、それぞれ粗補完財、粗代替財と呼ばれる。つまり各個人の趣向を無視した全体の傾向である。

簡単に言えば、補完財は仲間の関係で、代替財は敵対する関係。

3 需要供給曲線とワルラス均衡

一商品での需要供給に関する話と、加えて豊作貧乏のメカニズムを解説する。

3.1 市場の部分均衡

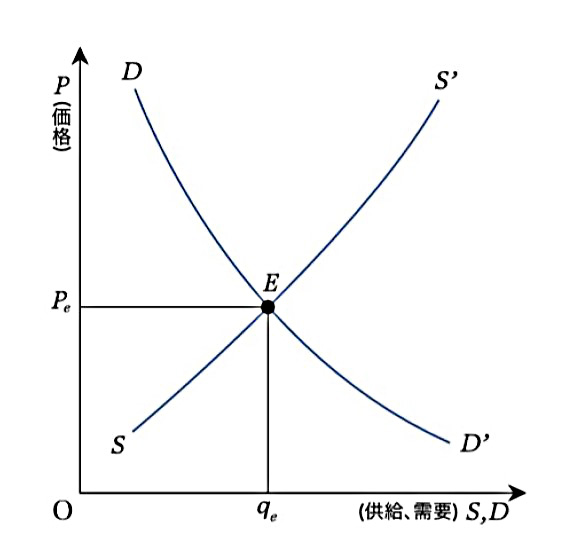
市場全体の需要関数$D(p,m)$と、供給関数$S(p)$を考える。

今回は1 商品なので代替性と補完性は無関係。$m$は固定し、$D(p)$と略記する。

$D,S$交わる点$p$を均衡価格という。

$D$は$p$に対して狭義単調減少、$S$は狭義単調増加なので、一般的には$p$ は一意。

3.1.1 ワルラス的調整

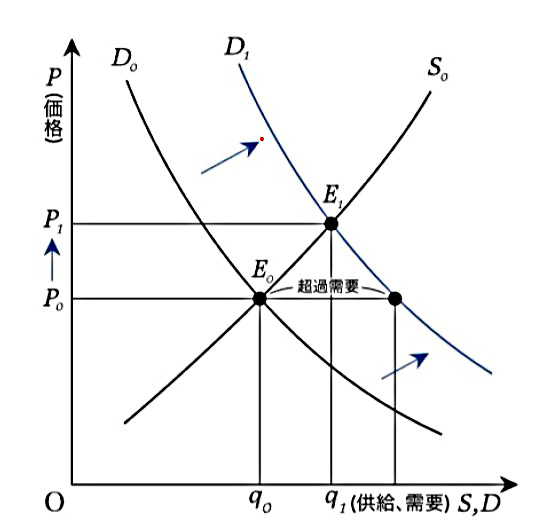
ここで、需要が増えた場合、$D_\phi(p):=D(p)+\phi(p)$ ($\phi$は正で広義単調減少) この場合は、$D_\phi(p) = S(p)$となる点$p_d$は$p$より大きくなる。これにより、需要超過の状態が再度均衡するも、値段が上昇する。

次に供給過剰の場合。$S_\phi(p) := S(p)+\phi(p)$ に変化した場合、$D(p) = S_\phi(p)$となる点$p_s$は$p$より小さくなる。これにより、供給超過の状態が再度均衡するも、値段が下落する。

これをワルラス的調整という。

3.1.2 マーシャル的調整

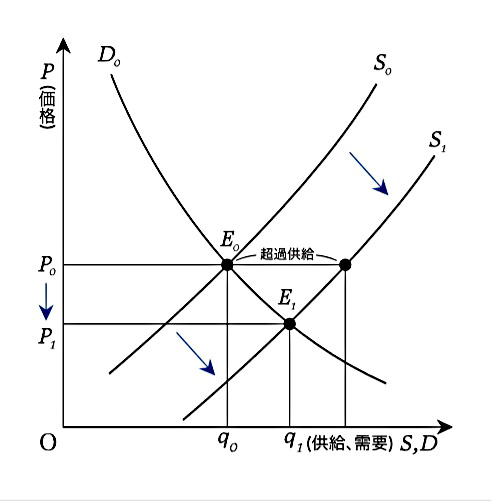
ワルラス的調整は市場の不均衡に対して、価格調整により対応が行われたが、一方で供給調整での調整もおこなわれる。

同じく$D_\phi(p) := D(p) + \phi(p)$($\phi$は正の単調増加関数)となった場合、供給を同じように$S_\phi(p) := S(p) + \phi(p)$と増加させることで、同じ点$p$によって均衡が成される。

このように、需要変化に対して供給変化で対応が成される市場を「安定した市場」と呼ぶ。

3.2 豊作貧乏

豊作により作物の供給量が増え、それによる価格下落で農家の利益が減ることを「豊作貧乏」という。

輸送コスト等の増大での売り上げ減少もさることながら、下記定理により、必需品の供給過多は、そのまま生産者の売り上げ自体が減少する。

先ほどの図を用いる。

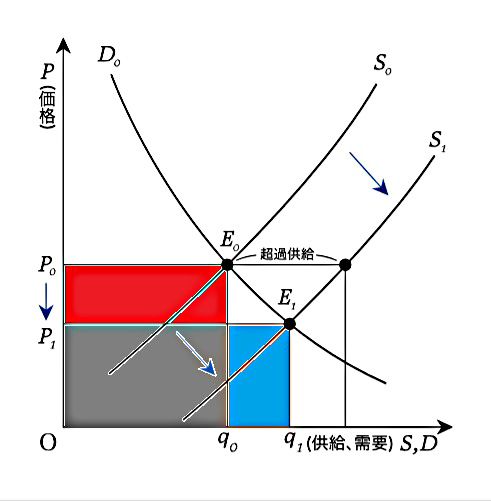
ここで、赤＋灰色部分は供給変化前の売り上げ。
青＋灰色が供給変化後の売り上げ。
赤い部分の面積を$A$、青を$B$とおく。

この面積を比較する。

豊作貧乏が起きる状況は$A > B$だが、これはすなわち$(P_0-P_1)q_0 > P_1(q_1 – q_0)$ということである。仮定より$q_1 -q_0$であるため、

$ \frac{P_0-P_1}{P_1}> \frac{q_1-q_0}{q_0} $

需要の価格弾力性$\epsilon$が$[P_1,P_0]$内で常に$1$より小さい場合、この式が成り立つ。

すなわち「価格の変化に対して需要の変化が小さい」場合に豊作貧乏が起きる。野菜のような不可欠な存在である。$^{\ast 5}$

必需品は供給過多が売り上げ減少に直結するわけだが、逆に言えば贅沢品は少しくらい値段下げてでも数さばいたほうがいいことがわかる。

特に農作物のような、供給量の調整が難しい$^{\ast 6}$生活必需品は、これが起きやすい。

よく小学校の社会科の教科書などで、豊作貧乏の解説で農作物を破棄している農家の画像があるが、これを行った農家には国からの補助金があてがわれる。$^{\ast 7}$

$^{\ast 5}$必需品であると言いたいが、厳密な定義では異なる。経済学用語ではなく日常単語としての「必需品」であると言うのが最も近い
$^{\ast 6}$農作物は性質上増産には1 年以上かかるうえ、作りすぎた場合破棄くらいしか調整手段がない
$^{\ast 7}$価格弾力性は当然一定ではない。あまりに供給を下げ値段を吊り上げすぎると、今度は代替効果で売り上げが減ると考えられる。

3.3 ダイナミックプライシング

価格調整と供給調整の話をしたが、いつも供給調整ができるわけではない。実際、それにより品薄や売れ残りといった状況が存在しうるのである。

実際の市場では価格や供給の調整は十分に働かないとする理論や実証も数多くある。なによりネックとなるのは、動的な価格付けが不可能な点。

それを解決する一助となるのが、ダイナミックプライシングの技術である。

この記事をシェアする