Miyamoto
1 扱った論文について
論文タイトルはMachine Learning Approximation Algorithms for High-Dimensional Fully Nonlinear Partial Differential Equations and Second-order Backward Stochastic Differential Equations
著者はChristian Beck,Weinan E,Arnulf Jentzen で、論文アクセプトは2018。
掲載誌はSpringer Sci- ence+Business Media, LLC, part of Springer Nature 2019
2 論文概要
2.1 モチベーション
2.1.1 偏微分方程式と確率微分方程式の関係、そしてその応用
まず、次のような偏微分方程式を考える。
(1)
次に、このような後退型確率微分方程式を考える。
(2)
とおくと、(1) より、確率1で次が成り立つ。(非線形ファインマンカッツの公式と呼ばれる。)
(3)
主にファイナンス分野では、オプション価格のプライジング等のタスクで、確率微分方程式に従う確率過程の、終端における値を関数に入力した値の期待値を求めることが必要とされてきていた。
非線形ファインマンカッツの公式の簡単な応用例としては、\(g\) をペイオフとして
(4)
と置くと\(u(t, x)\) は\(X_T\) が従う確率微分方程式の被積分関数を用いて構成できる放物型偏微分方程式に従う。
2.1.2 上記手法の限界
偏微分方程式の数値解析を用いる手法には大きな問題点がある。「次元が増えすぎると数値が不安定になり計算量も爆発する」という点だ。
例えば、空間が1 次元の時に空間を\(N\)分割する場合、\(d\)次元では\(N^d\)個の分割が必要になる。
実際には不安定性の解決のために、さらなる細かさが必要になってくる。(数値解析の手法にもよるが、どの手法でも次元増加による計算量増加のオーダーは概ね同じ)
かつて偏微分方程式の数値解析は物理学への応用を念頭に置かれて作られていた。
つまり空間は最大でも3 次元で済んだが、ファイナンスや機械学習、最適化など、近年の偏微分方程式の応用分野は、3 次元では対処しきれない。
例えばファイナンスでは\(d\)は株の銘柄の数であり、機械学習や最適化では\(d\)は特徴量の数であることが多い。すなわち、タスクによって際限なく大きくなりうる。
そこで、機械学習により、直にこの値を推定していくことを目指す。
2.2 具体的な手法概要
BSDE(Backward Stochastic Differential Equation:後退確率微分方程式の略)の初期値\(\xi\)を固定する(ファイナンスでいうところの「現在の株価」に相当する)。
その状況下で、\(f, g \)がすでに与えられている状況で\(u(t,x)\) の値を推定していく。
\(Xt := \xi +W_t\) とおく。
ニューラルネットで近似するのは\(At.\Gamma t\)、すなわち上記の定理より
(5)
\[\Gamma _t = (Hess_xu)(t, x)\]
(6)
というそれぞれの右辺にある二つの関数を求めれば、それはすなわち\(\Gamma t_,A_t\) を求めるに等しく、それを用いて\(Y_t,Z_t\) はオイラー丸山法で近似していくことができる。
時刻\(0 < t_1 < t_2 < …… < t_N = T \)とおき、それぞれの離散ステップ\(t_n\) 毎に、ニューラルネットで\((Hess_xu)(t_n, x),(\frac {\partial}{\partial t} \nabla _xu )(t_n, x) + \frac{1}{2} (\nabla _x \Delta _xu)(t_n, x) \)を構成する。
それぞれの関数構成は4層パーセプトロンを用いて、活性化関数はReluを使う。
さらに\(d + 1\)次元のニューラルネットで\(u(0,x);\nabla _xu(0,x)\)を構成する。
これらを利用し、\(N\)ステップのオイラー丸山スキームで\(Y_t,Z_t\)を近似していく。
また、それぞれの離散ステップの\(n\)ステップ目を\(\mathcal{Y} ^\theta _n,\mathcal{Z} ^\theta _n, \Gamma _{t_n}, A_{t_n}, W_{t_n}\)と表記する。
ニューラルネットのパラメータを全体を\(\theta\)と書く。
最適化においては、毎回ブラウン運動のサンプルパスを生成し、それに対して\(Y_t,Z_t\)などの強近似を行ったうえで
(8)
という形で損失関数を定義し、これに対する勾配を計算していくことで最適化を行う。考え方そのものはSGD である。
つまり、最初に解説した「確率過程の終端値を評価するにあたって、対応する偏微分方程式を解く」という歴史ある手法の真逆であり、「確率過程を機械学習によって直接近似する」というやり方である。
偏微分方程式との対応は、主目的が高次元の偏微分方程式数値解析である場合以外にも、評価を目的として利用することも可能である。
2.3 数値結果
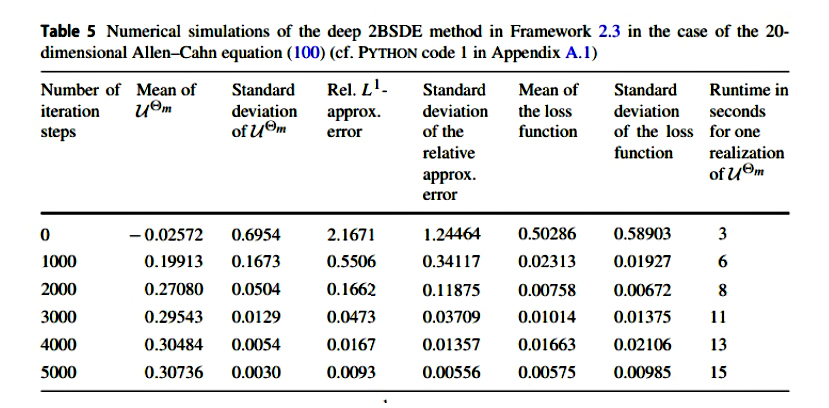
本論文では、解析解がすでにわかっているPDE(ブラックショールズ方程式) と、それに対応するBSDE に対して、上記手法での数値実験が行われている。
この数値結果を見る限り、全く新しい数値計算手法として、決して悪くないものであると考えられる。
3 改善案考察
ここからは、論文まとめではなく、論文を踏まえてどのような改良を施すかについて考察する。
\(u(t_n,x)\)と\(t_{n+1},x\)を全く別の関数として構成するのは、かなり効率が悪いと思われる。
なぜなら、小さく区切った\(t_n\) の変化によって、\(u(t_n, x)\) の値は一般的にはあまり変わらないといえるからである。(そこで大きく変化してしまうようなPDEの解は、そもそも数値解析などしようがない)
そのため、いくつか案が考えられる。
3.1 RNN を用いる
すなわち、\((Hess_xu)(t_n, x)\) の中間層から、あるアフィン変換した値(当然ここもパラメータを用いて学習する)を\((Hess_xu)(t_{n+1}, x)\)を近似するネットワークの中間層の値に足してしまうということである。
このように、\((Hess_xu)(t_n, \xi +W_{tn})\)を近似するときに構成した計算フローの値を、\((Hess_xu)(t_{n+1}, \xi +W_{t_{n+1}})\)の計算に用いることができ、短時間遡った値を大いに活かすことができる。
3.2 Smoothness loss
損失関数の設計に関する正則化の提案である。出典は[2]。
通常の平均二乗誤差に加え、時間ごとのパラメータ差分にペナルティをつける。
時刻\(t_n\) における関数のパラメータを\(\theta _n\) とおくと、3 章冒頭の考察により、\(\theta _n\) と\(\theta _{n+1}\) の値は近いほうが望ましい。
一定の正則化係数\(\beta\)を用いて
(8)
を損失関数に付け加える。
最善と思われる改善案は未公開論文の定理を含むため現段階では非公開とさせて頂きます。
参考文献
[1] Etienne Pardoux1,Shanjian Tang,Forward{backward stochastic differential equations and quasilinear parabolic PDEs. Probab. Theory Related Fields 114 123{150,1999
[2] Bo Chang,Lili Meng,Eldad Haber,Lars Ruthotto,David Begert,Elliot Holtham,Reversible Architectures for Arbitrarily Deep Residual Neural Networks,Published in AAAI 2017
