Koudai Satake
本記事について
比較的最近の論文で、旅行業界・航空業界でダイナミックプライシングを導入したという論文が出ていましたので、それについて解説します。
論文名: Dynamic Pricing for Airline Ancillaries with Customer Context
https://arxiv.org/abs/1902.02236
概要

航空業界において、付帯サービス運賃は今や重要な収益源となっています。付帯サービス運賃というのは、航空運賃とは別に、食事や事前座席指定、追加手荷物などの付帯的なサービスに課せられる料金のことです。
飛行中に受けられるサービスの他に、旅行プランに関係するサービスとして、ホテルの部屋、レンタカー、目的地で行う活動、に関連する場合もあります。
しかしながら、付帯サービス運賃の価格戦略は、慣例に基づいており、最適化が不十分です。
本稿では、旅行会社向けのAI技術提供会社である、ディープエアソリューションによって開発された動的価格決定モデルについて説明します。
このモデルは、予想収益を最大化するように、各顧客に合わせて、最適な付帯サービスの価格を提案します。
本稿では、付帯サービスの価格を動的に設定するためのアプローチを3つ提示し、比較します。
- GNBCを用いて需要予測を行い、ロジスティックマッピングを用いて価格決定を行う方法 (APP-LM)
- ディープニューラルネットワークを用いて需要予測を行い、網羅的に探索を行い、価格決定を行う方法 (APP-DES)
- ディープニューラルネットワークを用いて、一気に最適な提案価格を導出する方法 (End-to-End DNN-CL)
過去データを用いたオフラインでの評価と、実際に予約システムに導入した実験により、モデルの性能やビジネスへのインパクトを示します。
結果、機械学習技術の導入により、人間のルールベースで行う場合と比較してコンバージョン率を36%、収益を10%向上させ、効果があることを示しています。
また、ディープラーニングを使ったアルゴリズムが、この問題に対し、従来の機械学習技術よりも優れていることを、オフラインでの評価によって示しました。
DNN-CLモデルは現在、航空会社の予約システムに導入中です。
背景
付帯サービス運賃の市場は非常に大きく、2015年には全世界で590億ドルに達しています。これだけ大きな右肩上がりの市場であるにも関わらず、価格決定の方法は進歩していません。
こういった付帯サービスは、昔から提供されていた訳ではなく、近年登場・拡大したため、航空会社は顧客の付帯サービス選択についてほとんど知見がない上、これらのオプションは、個人の好みや旅程との相性の問題であるため、付帯サービスのコンバージョン率は5%未満と非常に低いのが現状です。
航空会社の予約サイトでのセッションの流れは、以下のようなものです。
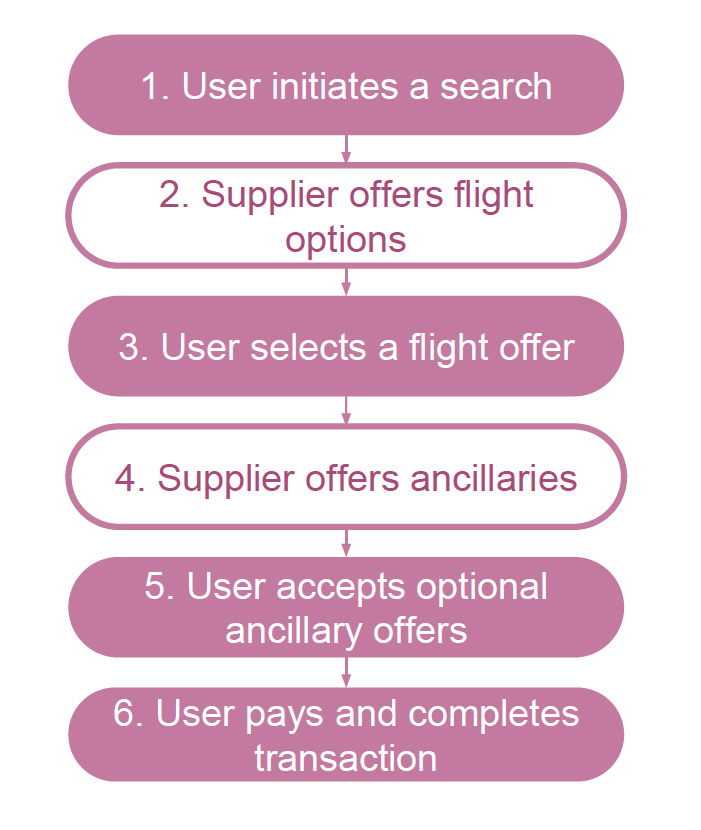
最初の3ステップで、出発地・目的地・座席といった、主なサービスを選択し、ステップ4以降で付帯サービスを選択します。
予約サイトでは、以下の様なシステムを用いています。
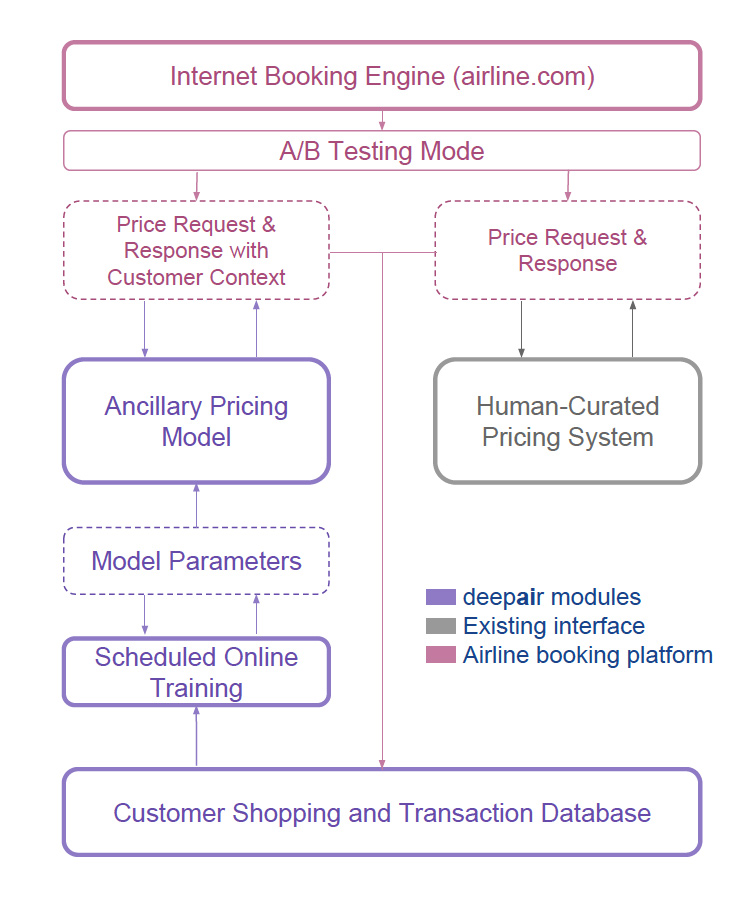
本稿での貢献は以下です。
- 既存の価格決定システムを収益面で上回る、各顧客に合わせた、付帯サービス向け動的価格決定システムを提供します。
- 顧客の支払い意欲の単調性をモデルに組み込むことにより、購入確率の効果的な推定と付帯サービスの最適価格を同時に導出する、ディープラーニングのモデルを開発しました。このモデルは、従来のように機械学習モデルと収益最適化を順に行うモデルよりも、正確に顧客の行動を捉え、収益を向上します。
- 本モデルは、比較対象と比べて、人間の選択をより正確に予測するため、付帯サービスのコンバージョン率が増加します。
- モデルを実装し、実データで評価した結果、精度向上を示しました。
価格決定に用いる要素
需要関数
まず、需要関数\(D(P)\)は、価格\(P\) の関数で、価格に対する需要の変動を推定することで得られます。次に、需要関数に基づいて予想収益を最大化する最適価格\(P^\ast\)を導きます。
(1)
\[P^{*}=\operatorname*{argmax P}_{P} \times D(P)\]
航空会社の付帯サービスの場合、需要関数は価格\(P\)だけでなく、顧客属性の関数でもあるため、顧客属性\(x\)を用いた需要関数 \(D(P,x)\)がより適切です。本稿では、2つの手法を比較し、顧客が薦められた付帯サービスを購入する確率を推定します。
顧客属性
顧客属性\(x\)は、その顧客が薦められた付帯サービスを特定の価格で購入する確率に影響を与える要因の集合です。需要関数が大きく影響を受けることがわかっている属性として主なものは、時間、市場、すでにカートに入っている商品、滞在期間です。
時間
(1)出発までの日数
通常、チケットを前もって購入する顧客は、出発に近い場所で購入する顧客よりも価格に敏感です。
(2)出発日時
チケット同様、付帯サービスも、時刻や季節との相関があります。ある特定の日時のチケットは、旅行時間の都合が良いだとか、接続が良いだとか、代替接続がないとか、特別なイベントがその日時であるとか、休日だとか、そういった要因により、需要が増大します。
それでもそのチケットを求める顧客というのは、価格に鈍感で、逆にそういったチケットを避ける人は、価格に敏感であるなど、ある特定の時刻や季節のチケットであるか否かは、集まる顧客タイプと強い関連があります。
市場
航空会社は、出発地と目的地で分類できる様々な市場に対してサービスを提供しています。特定の市場では、大部分が直行便ですが、他の市場では、乗り換えが必要な旅程が大部分であったりします。
一部の市場では出張の割合が高い一方、一部の市場では主にレジャーだったりします。そして、以下の図に示すように、他と比較して付帯サービスの需要が高い市場があり、どの市場であるかは、購入確率を推定するために重要です。
ここで、式(1)を使うために、これらの市場をさらにサブマーケットにセグメント化します。サブマーケットは、特定の付帯サービス価格に対する推定需要が統計的に類似する顧客集合ごとに分類します。
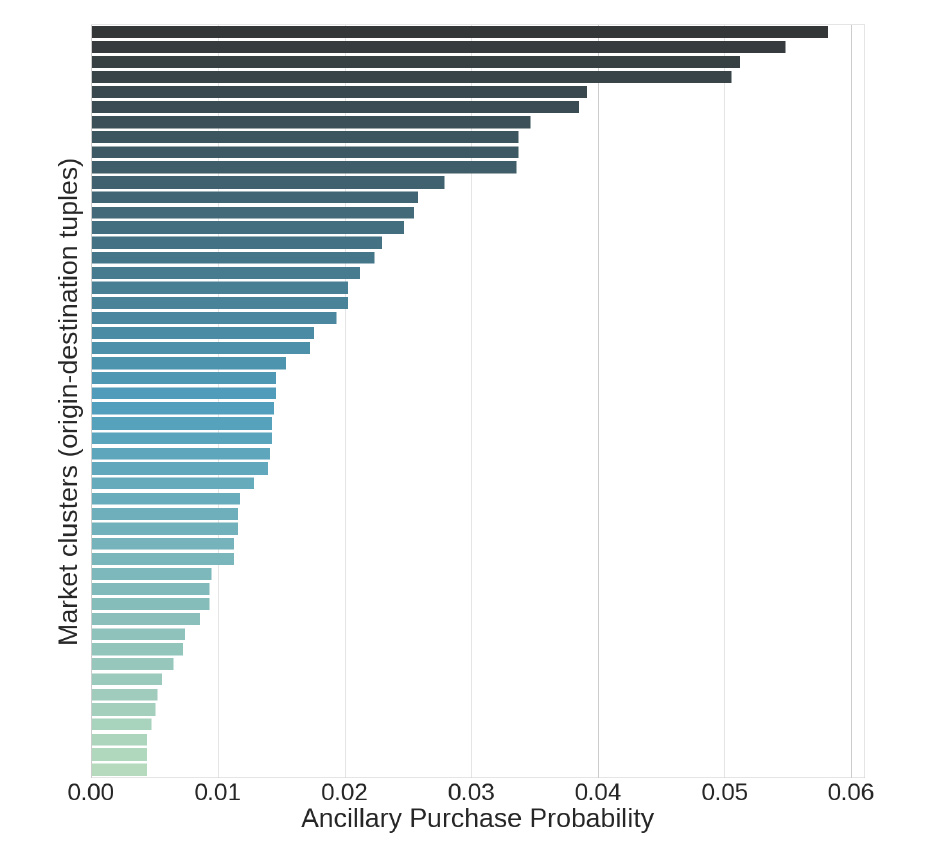
滞在期間
往復チケットの予約の場合、滞在期間(LOS)は、乗客が目的地に滞在する予定日数とし、片道チケット購入の場合、LOSは\(0\)とします。
以下の図は、2種類の予約について、LOSのカーネル密度推定(KDE)を示しています。全体と比較して、付帯サービスが購入された場合に限定すると、LOS値が中程度の箇所に偏っていることがわかります。
これは、LOSが中程度の乗客は、付帯サービスを購入する可能性が高いことを示しています。これは、例えば、乗客が追加の保管スペースを必要とする中程度の長さの旅行では、付帯サービスとして、バッグなどを購入したいと考えるためです。
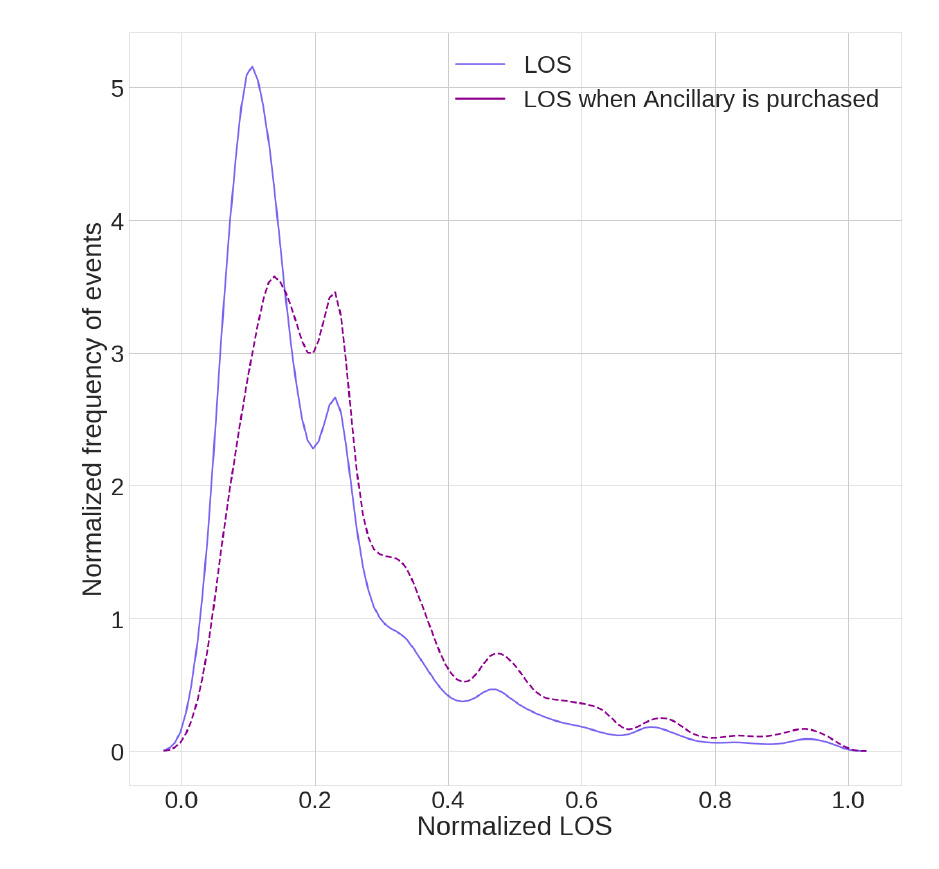
価格モデル
当社の価格設定モデルは、2つのブロックで構成されています。
- (i)付帯サービスの購入確率モデル
- (ii)購入確率を考慮して、予想収益を最大化する価格を提案するモデル
次のことを想定しています。
価格帯
提案される付帯サービス価格は、ビジネス戦略的に適切な範囲内でのみ変更します。
支払い意欲の単調性
ある顧客がある価格帯で製品を購入する意思がある場合、彼らはより低い価格で同じ製品を購入しようと思うはずです。
反対に、ある顧客がある価格で製品を購入しない場合、彼らはより高い価格で購入しようとは思わないでしょう。
本稿では以下の図のように、3つの異なる価格決定モデルを実装しています。
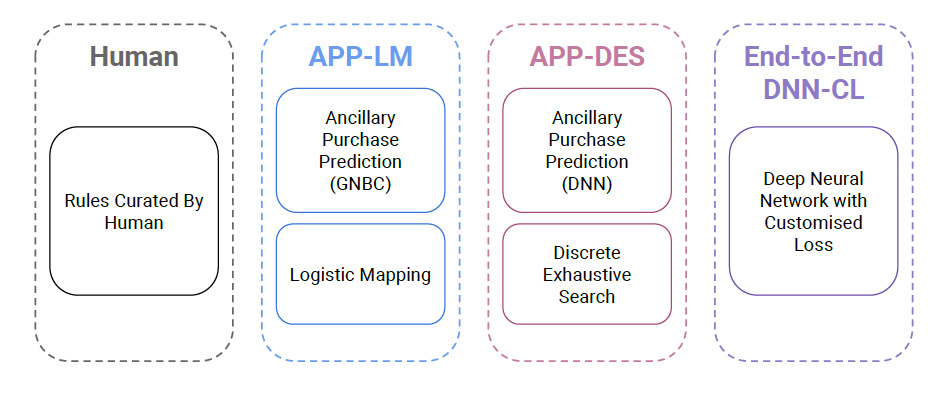
- GNBCを用いて需要予測を行い、ロジスティックマッピングを用いて価格決定を行う方法 (APP-LM)
- ディープニューラルネットワークを用いて需要予測を行い、網羅探索を使用して価格決定を行う方法 (APP-DES)
- ディープニューラルネットワークを用いて最適な提案価格を提案する方法 (End-to-End DNN-CL)
APP-LM、APP-DESでは、購入確率モデルと収益最適化モデルは順に用いていますが、DNN-CLではそれらを同時に求め、提示価格を提案します。
Ancillary Purchase Probability Model
確率モデルは、特定の付帯サービスに対して、特定の価格で特定のサブマーケット内の需要曲線を推定します。これは、二項分類問題を解くことで得ます。確率分布関数\(f_\theta(x,P)\)を推定することを目的としています。
ここで、\(x \mid x\subseteq x\)は特徴ベクトルで、\(P\)は提示された価格です。次のカテゴリに分類される30以上の特徴量を使用しました。
時間的な特徴
滞在期間、季節性(その日の時間、月など)、出発時間、到着時間、出発までの時間など。
市場固有の特徴
発着空港、発着都市、ルートにおける付帯サービスの人気度合いなど。
価格比較スコア:
同じクラスで同じ旅程の、他のチケットとの比較して、スコア化したもの
旅程固有の特徴:
予約人数、予約クラス、運賃、経由する空港の数など
前述したように、付帯サービス購入は非常に偏りが大きく (購入者は全体の6%)、非常に難しい二項分類問題となります。
APP-LMでは、主成分分析に基づいて選択された特徴を使用して、Gaussian Naive Bayes(GNB)、Gaussian Naive Bayes with clustered features(GNBC)、Random forest(RF)などの多くの伝統的な分類アルゴリズムを使って最初に比較評価します
APP-DESでは、クロスエントロピー誤差を用いて学習したディープニューラルネットワーク(DNN)を使用して、分類問題を解きます。
DNNは特徴量の加工をそこまで必要としませんでしたが、ネットワークアーキテクチャ、ドロップ率、アクティベーション関数、最適化アルゴリズム、収束基準などのさまざまなハイパーパラメーターを実験しました。
収益の最適化
ロジスティックマッピング
ベースモデルのAPP-LMでは、付帯サービスの購入確率が予測されると、ロジスティック関数を使用して、予測された確率に基づいて価格を決定します。
ロジスティックマッピングは、購入確率が高いほど付帯サービスの価格を最大値に近づけ、購入確率が低いほど、価格帯を最低値に近づけるという、直感通りの動きをします。
(2)
\[P^{r e c}=\frac{L}{1+\exp ^{-} k\left(x-x_{0}\right)}\]
上式では、3つのパラメータを用いて、関数を調整できます。
- 最大値\(L\): 付帯サービスの定価
- 形状係数 \( k \) : 曲線の形状・急勾配
- 中点 \( x _0 \) : シグモイド曲線の中間点
\(k、x_0 \) を使って、下図のように、価格設定を調整することができます。
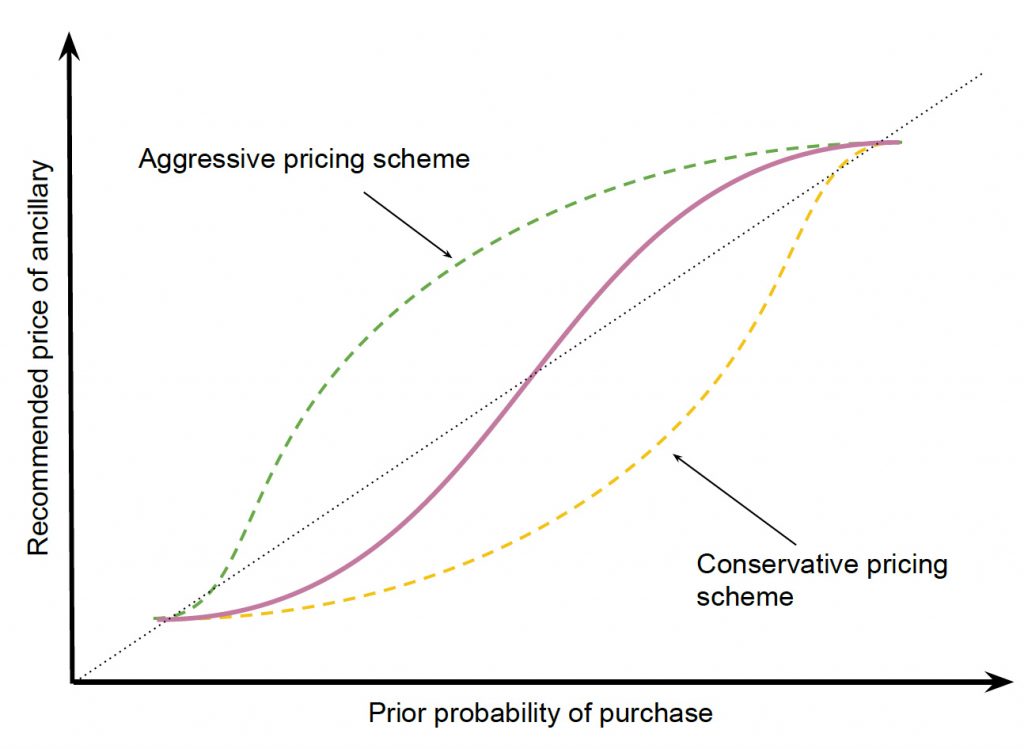
全探索
少ない価格点の集合を用いて、全探索を効率的に実行できます。 所定の購入確率\(f_\theta (x,P)\)と価格\(P\)に対して、期待収益は式(3)を用いて計算され、式4で表現される最適価格は、下図のように、全探索で見つけられます。
(3)
\[\hat{\mathbb{E}}{_P}=P \times f{_\theta}(x, P)\]
(4)
\[P^{r e c}=\underset{P}{\operatorname{argmax}} \hat{\mathbf{E}}_{P}\]
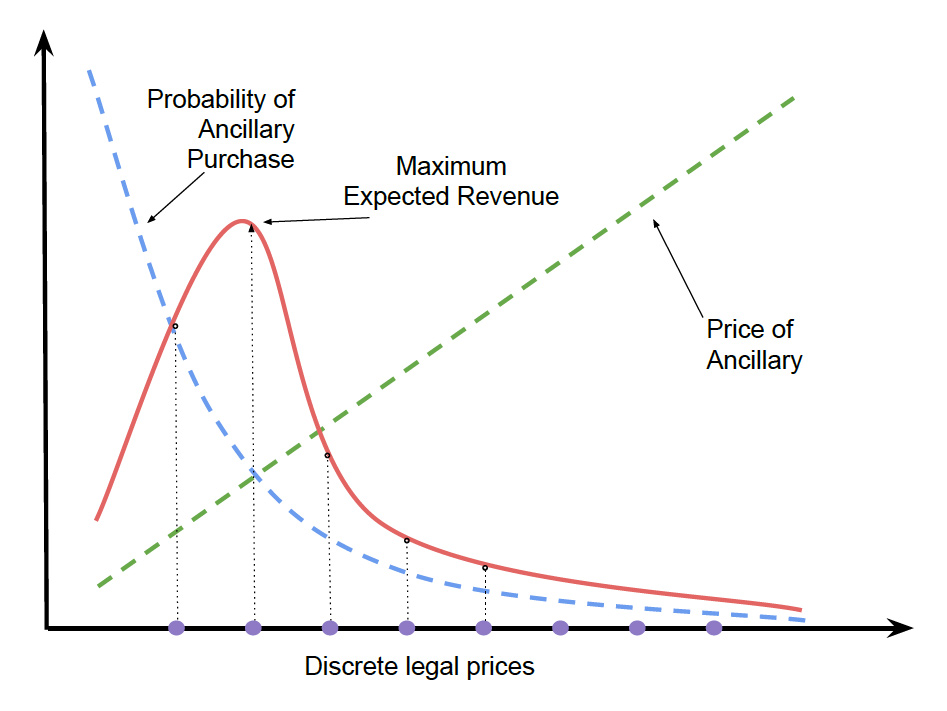
ただし、価格\(P^{rec}\)の最適性は需要予測の精度に依存します。需要予測結果に基づく、価格最適化手法 (APP-LMやAPP-DESなど) のパフォーマンスは、良好な需要予測に依存します。
良好な需要予測を行うためには、各サブマーケットの正確な価格感度を学習するために、各市場に対して十分なデータが必要です。
DNN-CLの損失関数
本節では、「購入されたので価格設定を低くしすぎたことに後悔するペナルティ」「高い価格を提示したことで購入されなかったペナルティ」を考慮した損失関数を示します。
考え方としては、\(N\)個ある学習データ( \(N\) パターンのセッションに対して、ある価格を提示して、実際に買ったのか買わなかったのかのデータ)と、適当なサンプル価格の集合Fがあり、各セッションの状況で、各サンプル価格が提示されていた場合、購入されていたかどうかを考えます。
あるセッションにおいて、ある価格で買われていた場合は、それより安くても買われていたはずで、ある価格で買われなかった場合は、それより価格が高くても買われなかったはずだと仮定することで、 \(N\) 個の学習データ(どの条件で、何円で提示したら買われたか否か)から、\(N^\ast \mid F \mid \)個のパターンに対して、買われたはず\(or\)買われなかったはず \(or\) 分からない、と言った結論が出ます。
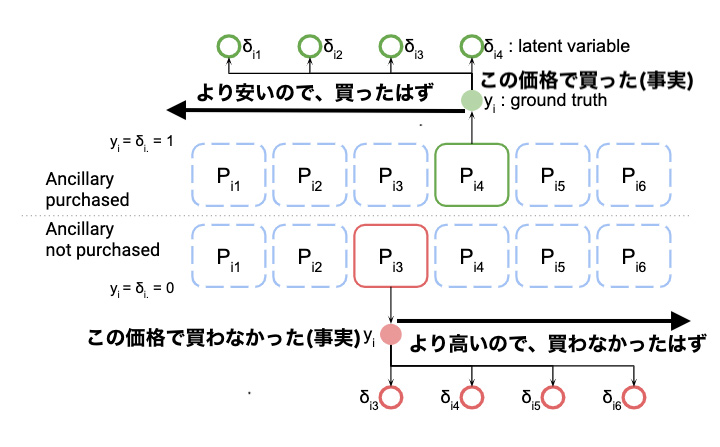
暫定提案価格よりも高い価格であるのにも関わらず、買われたはず、という結論が出たパターンに対しては、買われたその価格よりも暫定提案価格が安ければ安いほど、大きな損失を与えます。
逆に、暫定提案価格よりも安い価格であるのにも関わらず、買われなかったはず、という結論が出たパターンに対しては、買われなかったその価格よりも暫定提案価格が高ければ高いほど、大きな損失を与えます。
分からない、という結論が出たパターンについては考えません。
そのような損失関数を与えることで、結果的に、買われたという事実があるギリギリ高い価格を提案し、買われないという事実があるギリギリ安い価格を提案する方向に暫定提案価格が逐次更新されていきます。
これを数式で表現したのが以下になります。
学習データ: \(\{x_{i}, y_{i}\}_{i=1}^{N}\)
\(x_i\): 特徴ベクトル、\(y_i\): 正解ラベル(購入した場合\(1\)、非購入なら\(0\))
提案価格: \(P^{r e c}=F_Θ (x,F)\)
\(\theta\): 学習するパラメータ
\(F\): 離散的な価格点
以下の損失関数\(L\)を最小にする \(\theta\) を求めるよう学習
(5)
\[\mathcal{L}=\underset{\theta}{\operatorname{argmin}} \sum_{i=1}^{N} \sum_{j=1}^{| \mathbb{F} |}\left(\Phi_{l b}+\Phi_{u b}\right) \cdot \mathbb{1}{\left(\sigma{_{i j}}>0\right)}\]
\[\Phi_{l b}=\max \left(0,\left(L\left(P_{i j}, \delta_{i j}\right)-\mathbb{F}{_\Theta}\left(x{_i}, \mathbb{F}\right)\right)\right)\]
\[ \Phi_{u b}=\max \left(0,\left(\mathbb{F}{_\Theta}\left(x{_i},\mathbb{F}\right)-U\left(P_{i j}, \delta_{i j}\right)\right)\right) \]
(6)
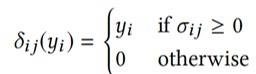
(7)
\[\sigma_{i j}=\left(j-j^{*}\right) \cdot(-1)^{y_{i}}\]
\(j^\ast\)は、セッション\(i\)に対して実際に提示した価格
(8)
\[L\left(P_{i j}, \delta_{i j}\right)=\delta_{i j} \cdot P_{i j}+\left(1-\delta_{i j}\right) \cdot c_{1} P_{i j}\]
(9)
\[U\left(P_{i j}, \delta_{i j}\right)=\left(1-\delta_{i j}\right) \cdot P_{i j}+\delta_{i j} \cdot c_{2} P_{i j}\]
モデル評価
これが最適であると言えるような価格や戦略がない以上、評価指標の定義は非常に重要です。オフライン指標は、モデル開発、インクリメンタル学習、ハイパーパラメーターの最適化に役立ち、オンライン指標は、実際のビジネス価値を測定します。
オフライン評価指標
ここでは、ハイパーパラメーターのチューニングに適し、DNNの重み更新がデータをover fittingしないような指標を定義します。
PDR
提示した価格が、購入されていない付帯サービスの現行価格よりも、どの程度安いか
PDP
購入されていない付帯サービスのうち、提示した価格が現行価格よりも低い割合
さらに、ReceiverOperating Characteristic(ROC)曲線のAUCをオフライン評価の指標として使用して、購入確率予測モデルのパフォーマンスを比較しました。
後悔スコア(RS)
最近の研究[21]では、後悔スコアは、ビジネス上の指標と比例するとのことで、オフライン評価基準として選択されています。
[21] Peng Ye, Julian Qian, Jieying Chen, Chen-hung Wu, Yitong Zhou, SpencerDe Mars, Frank Yang, and Li Zhang. 2018. Customized Regression Model forAirbnb Dynamic Pricing. In Proceedings of the 24th ACM SIGKDD InternationalConference on Knowledge Discovery & Data Mining. ACM, 932–940.
RSは式(10)で定義されます。
(10)
\[R S=\operatorname*{mean}_{p u r c h a s e s}\left(\max \left(0,1-\frac{P^{r e c}}{P}\right)\right)\]
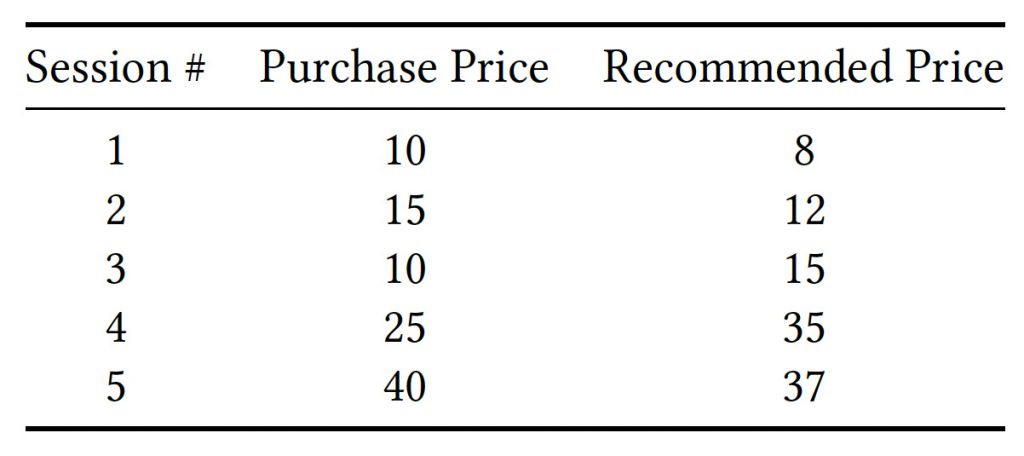
売れた際に、もっと高くしておけばよかったと後悔する度合いです。実際に購入された価格よりも、提示した価格が安ければ安いほど、上記の値は大きくなる(大きいと良くない)。
価格低下F1(PDF1)
このスコアは、精度の評価とトレードオフのトレードオフに使用されるF1スコアに触発されています。 したがって、PDF1は(11)に従ってPDRとPDPの間のトレードオフを測定します。
(11)
\[P D F 1=\frac{2 \cdot P D R \cdot P D P}{P D R+P D P}\]
オンライン指標
オンライン評価での指標は、モデルがビジネスの価値を向上させていることを示す指標を用います。
- コンバージョン率 Conversion Score =Number of purchases/Total number of sessions
- セッションあたりの収益
評価(実験)
オフライン評価
まずは、モデルの性能評価を行います。
- (i) 付帯サービスの購入有無の予測はどの程度正確か?(需要予測の精度)
- (ii) 需要予測と価格最適化を分けるモデルと、一気に最適価格を求めるモデルと、どちらがプライシング効果ありか
(i) 付帯サービスの購入有無の予測はどの程度正確か?(需要予測の精度)
評価指標としては、AUCを用います。評価結果は以下の通りです。
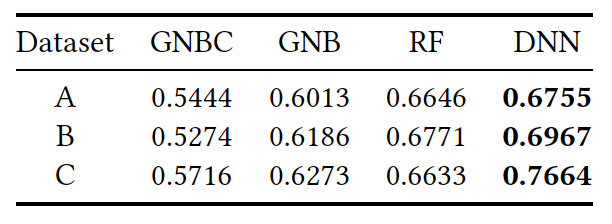
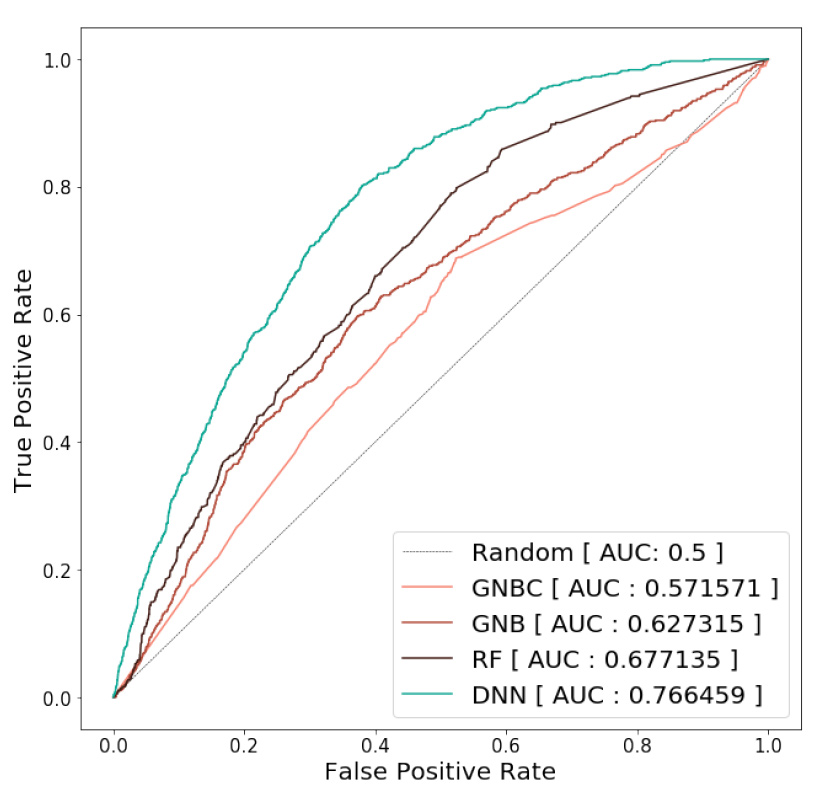
上記から、DNNがもっとも高い予測精度であることがわかります。
これは、特徴量とのより複雑な関係を、DNNが捉えることができているためです。
(ii) 需要予測と価格最適化を分けるモデルと、一気に最適価格を求めるモデルと、どちらがプライシング効果ありか
評価結果は以下の通りです。
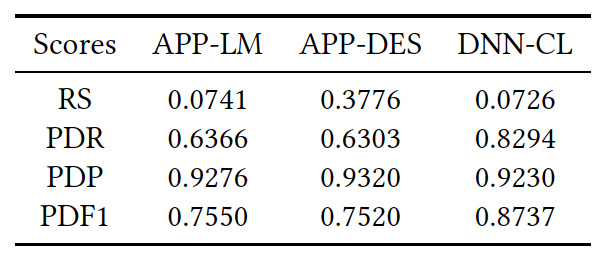
(もっと高い価格でも購入されていたはずなのに)安すぎる価格を提示していたことを示す値RSは、DNN-CL手法が一番低く、最良でした。
購入されなかった場合について、現行の価格よりも安い価格を提示していた割合を示すPFR,PDP,PDF1を見ても、DNN-CL手法が総じて良いことがわかります。
オンライン評価
オンライン実験の初段階では、「現在人が行なっている値付けよりも安い価格を提示する」という戦略をとった時にどうなるか、という点に着目して実験します。
これは、狙いを一点に絞ることで実験を簡単できるということもありますが、まずこの戦略をとったのは、ネットで事前購入した場合は安くなるという特典をつけることで、顧客との摩擦を減らせるから、という動機もあります(実験的に高くすると、顧客からの反発がある可能性があるということ)。
したがって、今回の実験の目的は、うまく割引を行うことで、1オファーあたりの平均利益を落とさずに、付帯サービスのコンバージョン率を改善できるか、ということになります。
比較手法には、現在の人が値付けする方法の他に、ランダムに値付けする方法も加えます。ランダム手法を入れる理由としては、以下です
・値下げによる、コンバージョン率変化の基準とするため
・様々な価格を探索し、価格感応度を比較するため
評価結果は以下です。
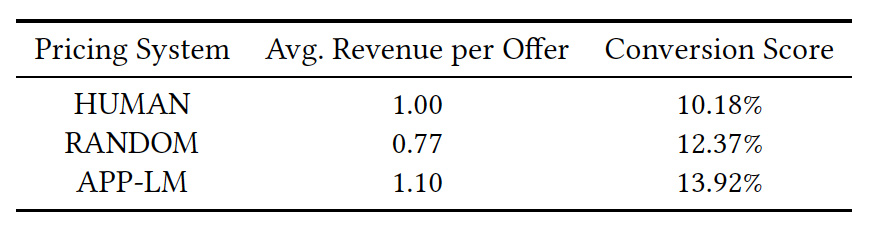
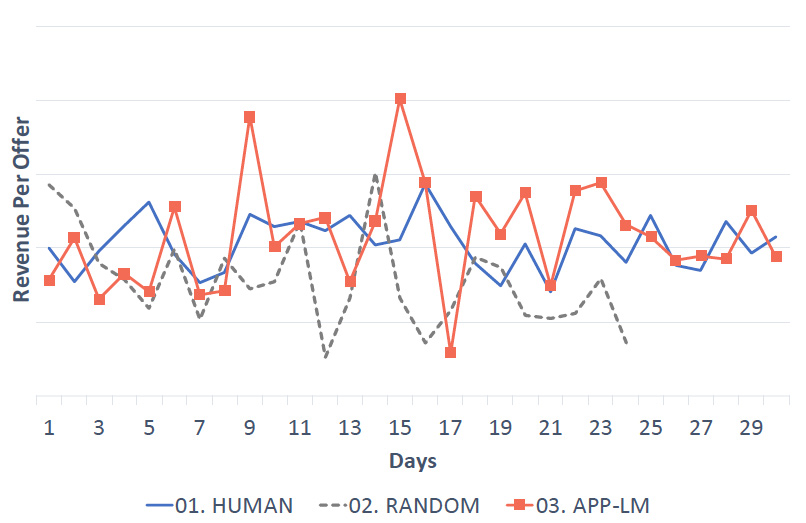
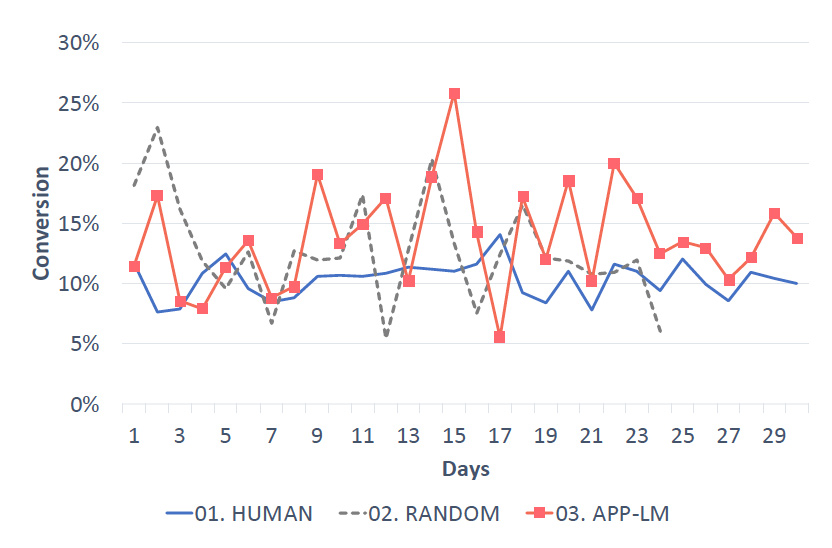
上記では、機械学習手法であるAPP-LMは、従来の手動やランダムと比較して、良い結果を出していることがわかります。
ランダム手法が1オファーあたりの平均利益を上げられないのは、顧客の性質(いわゆる前述のサブマーケット)を区別せずに一緒くたにしてしまって、その違いを識別できていないからです。
価格を下げたことに対する顧客の反応は、ランダムモデルでも当然見られるため、コンバージョン率自体はそこまで大きく変わらないのではないかと思われ、実際結果もその通りとなりました。我々の手法は、36%程度のコンバージョン率増加(ランダムと比較して15%の増加)と、10%の利益増をもたらしました。
すなわち、我々のモデルは、人間と比較して、収益を高く保ちつつも、コンバージョン率を上げることに成功しています。これは、モデルが市場の動向をタイムリーに掴めており、顧客の状況に応じた割引が正確にできていることを示しています。
所感
航空業界・旅行業界で、付帯サービスの価格に対して、ダイナミックプライシングを導入してみて一定の成果が出たという実例は、興味深いと感じました。
古典的な機械学習手法であっても、オンライン実験の結果は増益であり、これは顧客の価格感度を捉えられるだけの特徴量をうまく選ぶことができているということなのだと思います。
オフラインでの評価に関しては、評価指標がDNN-CLに与えているコスト関数にかなり寄っているような気はしましたが、本評価指標が妥当と考えるならば、最も得たい結果に近い学習を行なえているということだと思います。
DNN-CLの場合は、学習データを基にして「売れそうなら売れなくなるギリギリまで高い価格、売れなさそうなら売れるギリギリまで安い価格」を直接導きますし、学習データを基にして、その正答率が極力高くなるようなニューラルネットワークを形成しますが、他の2手法のように、確率の導出という過程を一度経由して価格を導出しまうと、確率を求めた時点で、情報が丸められてしまうことになるのではないかと思います。
例えば感覚的には、各状況に対して導出された確率は、状況によってその確率に対する確信度合いのようなものがあるはずです(ここでの確信度合いは、学習データに依存)が、\(D(P,x)\)を出した時点で、その情報は欠損しており、確信の度合いが低い場面における確率も、確信の度合いが高い場面における確率も一様に扱って、価格の探索を行ってしまいます。
同様の取り込みは、国内の同業界でも使えそうです。付帯サービスの価格決定にはもちろん使えますし、似た特徴を持つ商品に対しても、似たような手法が応用できそうです。
そのような取り込みを検討されているようでしたら、是非とも弊社がお役に立てれば幸いです。
