強化学習における報酬分布の近似アルゴリズムについて - ダイナミックプライシングテクノロジー developers lab

Miyamoto

コンテンツ

1 参考論文

An Analysis of Categorical Distributional Reinforcement Learning
https://arxiv.org/pdf/1802.08163.pdf

状態空間、行動空間ともに有限の状況で、SARSA 法を用いる強化学習の理論的解析を行っている。

本記事は、この論文の内容をまとめるとともに、確率論的に正しく厳密な表記に改良し、不足している証明の一部を補完したものである。

本記事内にて、付け加えた定理は「補完定理」と呼ぶ。

2 論文概説

2.1 notation

\(\mathcal{X} :\)状態の集合（有限集合）
\(\mathcal{A} :\)行動の集合（有限集合）
\( \mathscr{P}(B) : B\)が有限集合の場合は集合\(B\) 上の確率測度全体の集合。 \(B\)が無限集合の場合はボレル確率測度全体の集合
\(\pi:\)方策関数。\(x \in \mathcal{X}\)ごとに定まる\(\mathcal{A}\)上の確率測度
\(\mu : x \in \mathcal{X}, a \in \mathcal{A}\)によって定まる、即時報酬と遷移後の状態を司る確率測度\(\mathscr{P}(\mathbb{R} \times \mathcal{X})\)
\(\gamma :(0,1)\)に含まれる実数で、報酬の割引率。
\(\left(X_{t}, A_{t}, R_{t}\right) : \mathcal{X}, \mathcal{A}, \mathbb{R}\)上の離散時間確率過程。確率法則は\(\mu, \pi\)によって定まる
\(\eta_{\pi}^{x, a} :\)現在の状態が\(x\)で、行動\(a\)をとった場合の、方策\(\pi\)による報酬の合計の確率分布を表す確率測度。すなわち、対応する\(\mathbb{R}\)に値をとる確率変数\(R_{t}^{x, a,\pi}\)が存在し

(1)

\[ R^{x,a,\pi}_t := \sum ^\infty_{s=t} \gamma ^{t-s} r_s ^{xa} |X_t=x,A_t=a \]

\(f : \mathbb{R}\)上のボレル可測関数
\(f_{\sharp} \mu :\)任意のボレル可測集合\(B \subset \mathbb{R}\)に対して\(\mu(f^{-1}(B))\)となる確率測度
\(f_{\gamma, r} : \gamma x+r\)
\(\mathcal{T}^{\pi} :\)方策\(\pi\)に対するベルマン作用素。定義は任意のボレル可測集合 \(B \subset \mathbb{R}\) に対して

(2)

\[ (\mathcal{T}^ \pi \eta)^{x,a}(B) := \int _\mathbb{R} \sum_{x ^\prime \in \mathcal{X},a ^\prime \in \mathcal{A}} f_{r,\gamma | \sharp} \eta^{x,a} (B)\pi(a ^\prime | x ^\prime) dp(r,x ^\prime | x,a) \]

確率変数\(X_t,A_t,r_t\)を用いて次のようにも表現できる。

(3)

\[ \mathcal{T}^\pi P^{s,a,\pi}_t := r^{x,a}_t+ P^{X_{t+1},A_{t+1},\pi}_{t+1} \]

ただし\(r^{x,a}_t \)とは、状態\(x\)に対して行動\(a\)をとった場合の報酬の確率変数で、\(P^{x,a,\pi}_t\)は\(R^{x,a,\pi}_t\)を近似する確率変数である。

\(P_t\)をできる限り\(R_t\)に近づけることが、この論文及び記事の課題となる。

\(\mathcal{T}:\)制御型ベルマン作用素。方策によらないベルマン作用素 \(\mathcal{T}\) を次のように定義する。

(4)

\[ \begin{align} (\mathcal{T}\eta)^{x,a} (B):= \int _\mathbb{R} \sum_{x ^\prime \in \mathcal{X},a ^\prime \in \mathcal{A}} f_{r,\gamma | \sharp} \eta^{x,a^\ast(x \prime)} (B)dp(r,x^\prime | x,a)\hspace{5mm} \\ a^\ast(x ^\prime) := \max _{a^\prime \in \mathcal{A}} E[r^{x^\prime,a^\prime}] \end{align} \]

確率変数を用いて次のようにも表現できる。

(5)

\[ \mathcal{T}P^{x,a}_t := r^{x,a}_t + P^{X_{t+1},a ^\ast(X_{t+1})}_{t+1} \]

\(a^\ast\)の定義は上記と同様

\(C: \mathbb{R} \)上の\(K\)個の点の集合\( \{z_1, z_2,……, z _{K} \}\)
\(\mathscr{P}_p( \mathbb{R} ):p \geq 1\)によって定まる、\(\mathbb{R} \)上のボレル確率測度のうち\(\int_\mathbb{R} |x|^pdx < \infty\)となる確率測度の集合
\(\Lambda(\mu,\nu):\)周辺分布\( \mu,\nu \in \mathscr{P}(\mathbb{R} )\)を持つ\(\mathbb{R} ^2\)上の確率測度の集合、すなわち\( \lambda \in \Lambda(\mu,\nu)\)は、任意のボレル可測集合\(A \subset \mathbb{R} \)に対して

(6)

\[ \lambda(A, \mathbb{R})=\mu(A), \lambda(\mathbb{R}, A)=\nu(A) \]

\(d_p:\mathscr{P}_p( \mathbb{R})\)上のWasserstein距離

(7)

\[ d_{p}(\mu, \nu) :=\inf _{\lambda \in \Lambda(\mu, \nu)}(\int_{\mathbb{R}^{2}}|x-y|^{p} \lambda(d x, d y))^{1 / p} \]

\(l_2:\mathscr{P}_2( \mathbb{R})\)上のCramer距離。\(F_\mu\)を\(\mu\)に対する分布関数として

(8)

\[ l_{2}(\mu, \nu) :=((\int_{\mathbb{R}}\left|F_{\mu}(x)-F_{\nu}(x)\right|^{2} d x))^{1 / 2} \]

\(\mu^{\mathcal{X}×A}:x,a\)ごとに定まる確率測度\(\mu^{x,a}\in\mathbb{R} \)の集合。濃度は\(|X|×|A|。\)これらの集合を\(\mathscr{P}(\mathbb{R} )^{\mathcal{X}×A}\)と書く。
\(\overline d:\mathscr{P}(\mathbb{R} )^{\mathcal{X}×A}\)の元\(\mu^{^{\mathcal{X}×A}},\nu^{^{\mathcal{X}×A}}\)同士の距離。基準の距離d を用いて、次のように表現される

(9)

\[ \overline{d}\left(\mu^{\chi \times \mathcal{A}}, \nu^{\mathcal{X} \times \mathcal{A}}\right) :=\max _{x \in \mathcal{X}, a \in \mathcal{A}} d\left(\mu^{x, a}, \nu^{x, a}\right) \]

\(\delta_x:\)点\(x\)に集中するディラック制度
\(\mathcal{P}:\)ディラック測度の線形和で書かれる確率測度の集合
\(\mathcal{C}:\mathbb{R} \)上の\(K\)個の点。
\(\mathcal{P}^K_C:C\) 上の点に集中するディラック測度の線形和で表される確率測度の集合。
\(\Pi_C:\mathcal{P}\rightarrow\mathcal{P}^K_C\)の射影作用素。定義は後述。
\(\mathcal{\hat T}^{\pi}:\)実践した部分だけ値を更新するベルマン作用素。方策に寄らない場合も同様。定義は後述。
\(\alpha_t(x,a):\eta\)の更新幅。ロビンスモンローの条件を確率１で満たす。
\(\mathscr{P} (B):B\)が実数上のボレル可測集合であるとき、\(B\)に台を持つような確率測度の集合

2.2 手法解説

上述の通り、確率測度\(\mu\)は今の状態\(x\)と、とる行動\(a\)によって定まる、次の状態と即時報酬を司る\(\mathcal{X}×\mathbb{R} \)上の確率測度である。

この\((\mu,\pi)\)の組をMarkov decision processといい、定義から明らかにわかる通りマルコフ性を持つ。

推定困難ではあるが、裏で確実にこの強化学習問題を支配している確率測度である。

この測度については、noise termとの兼ね合いで実際には推定する必要がなくなる。

ここで、\(\mu,\eta\)は、任意の\(x^\prime, x,a\)に対して\(\int_\mathbb{R}|r|^p\mu(dr,x^\prime|x,a)\lt\infty,\int_\mathbb{R}|r|^p\eta^{x,a,\pi}(dr)\lt \infty\)が成り立つとする。\(^{*1}\)

\(^{*1} \: \)論文に記載はないが、この仮定は論文に書かれていない必須の条件である\(\mathcal{T}^\pi\eta\in\mathscr{P}_p(\mathbb{R})\)を言うにあたって、非常に自然かつ簡易な仮定である。この仮定を置けば、上述のベルマン作用素の確率変数表記と三角不等式、\(|X|\lt \infty\)という根本的な仮定から、この必須条件は自明である。後にパラメトリックな分布で近似するにあたって、論文に記載されているディラック測度や正規分布を用いた近似では、任意の\(\eta _t\)はこの仮定を満たすことが容易にわかる。

補完定理 1

任意の\(p \geq 1\) に対して\((\mathscr{P}^{\mathcal{X×A}}(\mathbb{R}),\overline d_p)\)は可分バナッハ空間
proof.
\((\mathbb{R},d)\)は完備可分距離空間であるため、\(\mathscr{P}(\mathbb{R})\)はラドン測度の集合となり、Wasserstein 距離が定義でき、\((\mathscr{P}_p(\mathbb{R}),d_p)\)も完備可分であることが言える。

2.2.1 完備性

\((\mathscr{P}_p(\mathbb{R}),d_p)\)がバナッハ空間であるため、コーシー列\(\{\mu_n\}\)に対して、ある元\(\mu\)が存在し、任意の\(\epsilon\)に対して、自然数\(N\)が存在し、\(N \lt n\)となる任意の\(n\)に対して、\(d_p(\mu_n,\mu) \lt \epsilon\)となる。

\(\{\mathcal{M}_n^{x,a}\}\)がコーシー列であるということは、任意の\(x,a\)に対して、任意の\( \epsilon_p \gt 0\)に対してある\(N_{x,a}\)が存在し、\(N_{x,a}\lt n,m\)となる\(n,m\) に対して\(d_p(\mu ^{x,a}_n,\mu^{x,a}_m)\lt\epsilon_p\)が成り立つ。

この時、\((\mathscr{P}_p(\mathbb{R}),d_p)\)の完備性から、任意の\(x,a\)に対してある元\(\mu^{x,a}\)が存在し、任意の\(\epsilon_k \gt 0\)に対して、ある\(N^k_{x,a}\)が存在し、\(N^k_{x,a} \lt n \)となる任意の\(n\)に対して\(d_p(\mu^{x,a}_n,\mu^{x,a})\lt \epsilon_k\)が成り立つ。

ここで、\(\mathcal{X},\mathcal{A}\)が有限集合であるため、\(N^k_{x,a}\)は\(x,a\)に対する最大値が必ず存在しその値を\(N_{max}\)と書く。

\(\mu := \{\mu^{x,a}\}_{x,a}\)とおくと、上記の\(\epsilon_k \gt 0\)に対して\(N_{max} \lt n \)となる\(n\)に対しては\(\overline d_p(\mu_n,\mu)\lt \epsilon_k\)が成り立つ。

よって任意のコーシー列になかでの収束先があることが示せたので、完備性が成り立つ。

2.2.2 可分性

\((\mathscr{P}_p(\mathbb{R}),d_p)\)がバナッハ空間で、あることを利用し、\((\mathscr{P}_p(\mathbb{R})^{ \mathbb{X}× \mathbb{A} },\overline d_p)\)可分であることを示す。

前者が可分なので、可算集合\(S\subset\mathscr{P}_p(\mathbb{R})\)が存在し、任意の\(b_n\in\mathscr{P}_p(\mathbb{R})\)に対して、\(\{s_n\}\subset S\)を適切にとることで、\(d_p(s_n,b)\rightarrow 0\)が成り立つ。

そのため、任意の\(b^{x,a}\)に対して、\(\{s^{x,a}_n\}\)が存在し、\(d_p(s_n,b^{x,a})\rightarrow 0\)が成り立つ。

なので、任意の\(\mu := \{\mu^{x,a}\}_{x,a} \in \mathscr{P}_p(\mathbb{R})^\mathcal{X,A}\)に対して、集合族列\(\mu_n:=\{s^{x,a}_n\}_{x,a}\)をとれば、任意の\(\epsilon_e\gt0\)に対して\(x,a\)ごとに\(N_{x,a}\)が存在し、上記同様有限集合ゆえに\(N_{x,a}\)に最大値\(N^e_{max}\)が存在するため、それより大きい\(n\)に対して、\(\overline d_p(\mu_n,\mu)\lt\epsilon\)が成り立つ。

補題 1

\(\mathcal{T}^\piは\mathscr{P}_p\)において縮小写像(すなわち\(\mathscr{P}_p^{\mathcal{X}×A}\)上の作用素\(\mathcal{T}^\pi_{\mathcal{X}×A}\)も同様。) さらに\(\mathcal{T}^\pi\eta_\pi=\eta_\pi\)が成り立ち、バナッハの不動点定理より、任意の\(\eta_o\in\mathscr{P}_p\)に対して

(10)

\[ \left(\mathcal{T}^{\pi}\right)^{m} \eta_{0} \rightarrow \eta_{\pi} \quad \text { in } \quad \overline{d}_{p} m \rightarrow \infty \]

proof.

(11)

\[ d_{p}\left(\mathcal{T}^{\pi} \mu, \mathcal{T}^{\pi}\eta\right)= d_{p}(\int_{\mathbb{R}} \sum_{x^{\prime}, a^{\prime}} \pi\left(a^{\prime} | x^{\prime}\right) p\left(d r, x^{\prime} | x, a\right) f_{r, \gamma| \sharp}\mu, \int_{\mathbb{R}} \sum_{x^{\prime}, a^{\prime}} \pi\left(a^{\prime} | x^{\prime}\right) p\left(d r, x^{\prime} | x, a\right) f_{r, \gamma| \sharp} \eta) \]

(12)

\[ \leq \int_{\mathbb{R}} \sum_{x^{\prime}, a^{\prime}} \pi\left(a^{\prime} | x^{\prime}\right) p\left(d r, x^{\prime} | x, a\right) d_{p}\left(f_{r, \gamma | \sharp} \mu, f_{r, \gamma | \sharp} \eta\right)\quad(三角不等式) \]

(13)

\[ \leq \int_{\mathbb{R}} \sum_{x^{\prime}, a^{\prime}} \pi\left(a^{\prime} | x^{\prime}\right) p\left(d r, x^{\prime} | x, a\right) \gamma d_{p}(\mu, \eta)\quad(下記参照) \]

(14)

\[ =\gamma d_{p}(\mu, \eta) \]

ここで、途中の不等式\(d_p(f_{r,\gamma|\sharp}\mu,f_{r,\gamma|\sharp}\eta)\leq\gamma d_p(\mu,\eta)\)について補完する。

\(f_{r,\gamma}\)が、\( \gamma \)が0でない場合は全単射なので、\(g:\mathbb{R}^2\rightarrow\mathbb{R}^2\)とおくと、\(g(x,y)=(f(x),f(y))\)とおくことで、\(g_\sharp\lambda\in \Lambda\)が成立する。

wasserstein 距離の定義より、任意の\(\lambda\in \Lambda\)に対して、\(d_p(\mu,\eta)\leq(\int_{\mathbb{R}2}|x-y|^p\lambda(x,y))^{-p}\)が成り立つ。

任意の\(\lambda\in\Lambda\)に対して、

(15)

\[ d_{p}\left(f_{r, \gamma | \sharp} \mu, f_{r, \gamma | \sharp} \eta\right) \leq(\int_{\mathbb{R}^{2}}|x-y|^{p} g_{\sharp} \lambda(x, y) ) ^{-p} \]

右辺を変形し

(16)

\[ (右辺)=\gamma(\int_{\mathbb{R}^{2}}|x-y|^{p} \lambda(x, y))^{-p} \]

これが任意の\(\lambda\in\Pi(\mu,\nu)\)に対して成り立つため

(17)

\[ d_{p}\left(f_{r, \gamma | \sharp} \mu, f_{r, \gamma | \sharp} \eta\right) \leq \inf _{\lambda} \gamma(\int_{\mathbb{R}^{2}}|x-y|^{p} \lambda(x, y))^{-p} \]

(18)

\begin{equation} \leq \gamma d_{p}(\mu, \eta) \end{equation}

さらに\(\mathcal{X,A}\)が有限集合であるため、補完定理１と同様に\((\mathcal{P}_p,d_p)\)での縮小性が言えるということは、\((\mathcal{P}^{\mathcal{X×A}}_p,\overline d_p)\)での縮小性が言える。

最後に、\(\eta_\pi\)が\(\mathcal{T}^\pi\)に対する不動点であることを示せば、バナッハの不動点定理による収束が言える。

\(\eta_\pi\) に対応する確率変数を\(R^{ﾞ\cdot,\cdot,\pi}\)として

(19)

\[ \mathcal{T}^{\pi} R_{t}^{x, a, \pi}=r_{t}^{x, a}+\gamma R_{t}^{x, a, \pi} \]

(20)

\[ =r_{t}^{x, a}+\gamma \sum_{s=t+1}^{\infty} \gamma^{s-t-1,} r_{t}^{x_{t+1}, a_{t+1}} \]

(21)

\[ =R_{t}^{x, a, \pi} \]

ただし、\(x_{t+1}\)は\(x_t,a_t\)から分布が定まる確率変数で、\(a_{t+1}\)は\(x_{t+1,\pi}\)から分布が定まる確率変数である。

このマルコフ性\(^{\ast2}\)が不動性の証明において重要である。

定義 1

\(\mu\in\mathcal{P}\)に対し、その射影\(\Pi_C\mu\in \mathcal{P}^K_C\)を次のように定義する。

\(C:=\{z_1,z_{2_{……,}z_K} \}\)という順序集合に対して、

(22)

\[ \mu=\sum_{n=1}^{N} p_{n} \delta_{y_{n}} \]

(23)

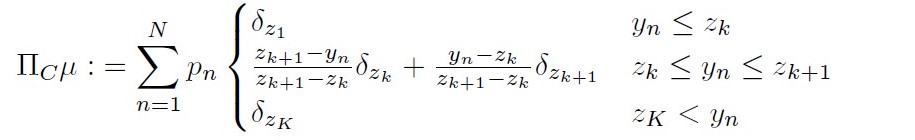
さらに次のSGD 的簡略化により、計算量を削減する。

定義 2

(24)

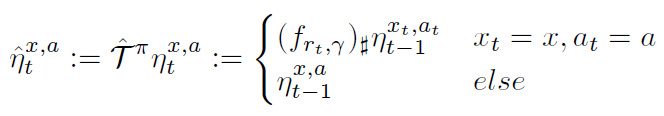
\(\Pi_C\mathcal{T}^\pi\)は残念ながらWasserstein 距離に対して縮小写像ではない。Cramer 距離に対しては縮小であるため、\(^{\ast3}\)それを利用する。

定理 1

\(\eta_C:=\inf_{\eta\in\mathcal{P}^K_C}\overline l_2(\eta,\eta_\pi)\)を置く。

\(^{\ast2}\)時刻\(t\)での報酬の確率分布が今の状態\(x_t\)ととる行動\(a_t\)によってのみ決定され、過去の状態や行動\(x_{t-1}\)などは関係ないという仮定

\(^{\ast3}\)よって三角不等式より\(\Pi_C \hat{\mathcal{T}}^{\pi}\)に対しても縮小

さらに、更新幅\(\alpha_t(x,a)\)を確率1で次の条件を満たすよう定義する。

(25)

\begin{equation} \sum_{t=1}^{\infty} \alpha_{t}(x, a)=\infty \end{equation}

(26)

\[\sum_{t=1}^{\infty} \alpha_t(x, a)^{2} < C < \infty \text{ for all }x, a\]

これはロビンスモンローの条件と言われる。例えば、\(\alpha_t(x,a)= 1/t\)とすると、これは条件を満たす。

この時、次のように測度\(\eta_t\)に対応する確率変数\(P_t\)を更新する。

(\(\hat \eta_t\) に対応する確率変数を\(\hat P_t\)と書く。\(\Pi_CP\)は、確率変数\(P\)に対応する確率測度\(\eta\)を用いて、\(\Pi_C\eta\)と書ける測度に対応する確率変数を表す。 \(\mathcal{T}^\pi\) に対しても同様。\(^{\ast4}\))

元の論文ではここは\(P_t\)ではなく\(\eta_t\)だが、確率測度同士の足し算は一般には成立しない。

もちろん対応する確率変数同士の足算は成立するため、ここではそれによって表記することにする。

(27)

\begin{equation} P_{t+1}^{x, a, \pi}=P_{t}^{x, a, \pi}+\alpha_{t}(x, a)\left(P_{t}^{x, a, \pi}-\Pi_{C} \hat{P}_{t}^{x, a, \pi}\right) \end{equation}

この時、次の収束が\(\overline l_2\)で成り立つ

(28)

\begin{equation} \overline{l}_{2}\left(\eta_{t}, \eta_{C}\right) \rightarrow 0(t \rightarrow \infty) \end{equation}

上の更新式は次のようなこのアルゴリズムは次のような数式で導出されている。

(29)

\begin{equation} P_{t+1}^{x, a, \pi}=P_{t}^{x, a, \pi}+\alpha_{t}(x, a)\left(\left(\Pi_{C} \mathcal{T}^{\pi} P_{t}\right)^{x, a, \pi}-P_{t}^{x, a, \pi}\right)+\alpha_{t}(x, a)\left(\Pi_{C}\left(f_{r, \gamma}\right)_\sharp P_{t}^{x^{\prime}, a^{\prime}, \pi}-\left(\Pi_{C} \mathcal{T}^{\pi} P_{t}^{x, a, \pi}\right)\right) \end{equation}

第二項は通常の更新項。ただしこれだけだと計算量が多く汎化も怪しい。

そこで第三項のノイズ項が加わる。SARSA 法的にランダムに方策を選び、SGD 的な最適化を行う。ベルマン作用素の定義より明らかにここは不偏性を持つ。

こうすることで、汎化性能を上げつつ、計算量を劇的に減らすことができる。

\(^{\ast 4}\)確率測度と確率変数は同一の存在なので特にこの注意は必要ないが、この資料の可読性向上のため書いた

2.3 紹介しなかった定理

また、最適行動戦略\(\pi_\ast\)に対する報酬の確率測度\(\eta_\ast\)の近似\(\eta _C\)は、上記のアルゴリズムの軽微な変更により一定の条件下でCramer 距離の下で到達可能であると論文には記されている（定理２）。

しかし、証明はともかく、この条件そのものがill-defineではないか？

という疑念が浮上し、その真偽がまだ不明であるため、この記事では詳細は解説しない。

2.4 今後の展望

弊社は、このアルゴリズムのダイナミックプライシングへの応用を行うと共に、理論・アルゴリズム両面から、この論文からさらに発展させる研究を行う予定である。

そのため、\(\mathcal{P}\)が任意の\(\mathcal{P} \geq 1\)に対し\(\mathscr{P}_p\)で稠密である証明や、種々の定理のCramer 距離での証明やり直しなど、我々が証明した定理のうちいくつかは、残念ながらこの記事に書くことができなかったが、論文を出すにあたっては解説記事としてその定理の数々を別記事に記載する予定である。

3 Appendix

最後に、\(\eta_C\)での近似誤差に関する定理を紹介する。

補題2 \(\eta_\pi\)が\([z_1,z,_K]\)に台を持つ場合。

(30)

\begin{equation} \overline{l}_{2}\left(\eta_{C}, \eta_{\pi}\right) \leq \frac{1}{1-\gamma} \max _{i}\left(z_{i+1}-z_{i}\right) \end{equation}

\(\delta\)が存在し、\(\eta_\pi\)が\([z_1-\delta,z_K+\delta]\)に台を持ち、\(\eta_pi(z_1-\delta,z_1)\cup(z_K,z_K+\delta)\leq q)\)の場合。

(31)

\begin{equation} \overline{l}_{2}\left(\eta_{C}, \eta_{\pi}\right) \leq \frac{1}{1-\gamma}\left(\max _{i}\left(z_{i+1}-z_{i}\right)+2 \delta q\right) \end{equation}

参考文献

[1] 確率測度の空間の幾何学, 太田慎一

この記事をシェアする