Makoto Kirihata
中古品市場について
メルカリなどのフリマアプリが急速に普及するなど、近年リユース市場が注目を集めている。
環境庁の調査[1]によると、2015年度の市場規模は3兆1千億円と言われており、すでに大きな市場であるが、フリマアプリ等の普及により今後ますます増加していくと思われる。リユース市場はリユースショップ、インターネットオークションが大きなプレイヤーで近年はフリマアプリが勢力を拡大している。
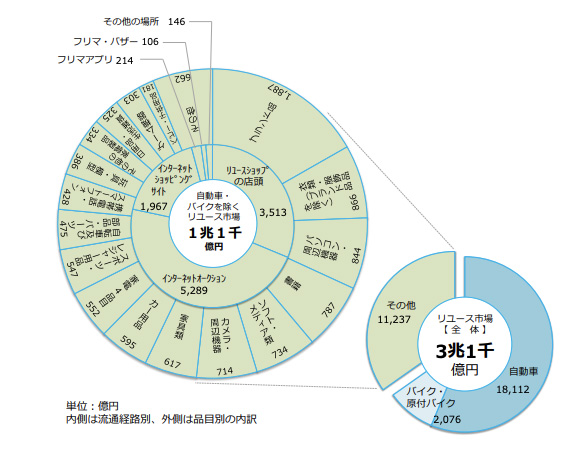
図1. 2015年度のリユース市場規模とその内訳(環境庁の調査 p.20[1]より引用)
http://www.env.go.jp/recycle/circul/reuse/confs/tokuhon_2.pdf
メルカリが行った中古品に対する意識調査[2]では、図2のような結果になり、中古品市場における価格の設定が極めて重要であることがわかる。
また、品質や信頼性も重要視されていることから、中古品の状態に対して適切な価格を設定することが必要である。
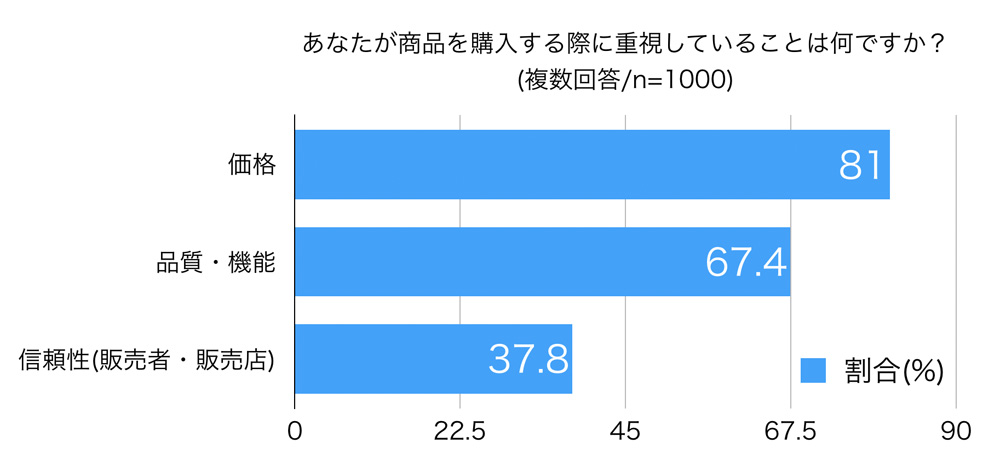
([2]におけるデータより作成)
現状、リユースショップの価格設定は人手で行っていることが多いが、とてもコストがかかることであるため、自動化することが望まれている。
そこで、今回は機械学習によるダイナミックプライシングの中古品への適用について調べた。
ビジネスへの適用事例
リクルート
リクルートマーケティングパートナーズは中古車市場における仕入れ車両の選定や仕入れ値、売値の判断をサポートする「D-MATCH」というシステムを開発した[3]。
D-MATCHでは、車種や価格、走行距離などの車両に関するデータと販売形態や地域などの店舗データ、さらに需給バランスなどのデータを組み合わせて、ある中古車をある価格で自分の店舗で売った時にどれくらい売れやすいかという成約率を予測する。
この成約率を色々な価格について調べたり、相場の情報を調べることで、その時々で、一番利益が出せる価格で買取、販売をすることが可能になる。
メルカリ
メルカリでは、実際に価格を動的に変更しているわけでないが、商品を売りたいと思った時に、出品者に売れそうな価格を推薦してくれる機能がある。
これに関連して、メルカリはデータ分析コンペティションであるKaggleにおいて、Mercari Price Suggestion Challengeというタイトルで自社コンペを開催している[4][5]。
コンペは、各商品の商品名やブランド名、カテゴリ、実際に購入された価格などの様々なデータが与えられており、新たな商品に対していくらで売れるかを予測するというものである。
1位のチームの手法は、MLP(Multilayer perceptron)でアンサンブルを行ったもので、その予測誤差は実運用にも耐え売る精度だった。
研究事例
ビジネスでの適用例は主に需要予測に基づいたダイナミックプライシングだったが、リユースショップでは単純な需要に合わせたプライシングではなく、在庫管理も含めたプライシング戦略が必要である。
リユースショップと少し毛色が違うが、車のエンジンの再製造会社(Remanufacturing firm)における在庫管理を考慮したダイナミックプライシング戦略に関する研究[6]について説明する。
再製造会社はユーザーから回収した製品を使用して、再製造製品を作り、市場価格で販売する。
回収数をコントロールするために、在庫の状況にしたがって、回収の値段を動的に調整することが必要。
問題設定
回収個数は\(\lambda(𝑎)\)をパラメータとしたポアソン過程に従うとする。
\(\lambda(𝑎)\)は提示された価格\(𝑎\)に依存し、\(𝑎\)が増加すると\(\lambda\)も増加する一対一の関係にあるとする。
同様に再製造された商品の需要が\(\lambda(𝐷)\)をパラメータとしたポアソン過程に従うとする。
回収にかかるコストと商品を保管するのにかかるコスト、さらにLost salesという在庫がなく需要に答えられないという機会損失のようなコストを考える。
\(a(t)\)を\(t\)における価格、\(N(t)\)を\(t\)における回収数、\(h\)を保管にかかる単位コスト、\(x(t)\)を\(t\)における保管数、\(𝑐𝑙\)をLost salesの単位コスト、\(Y(t)\)を需要個数とした時、期間\(T\)における期待コストは以下の式で求められる。
この時、\(N(t)\)と\(Y(t)\)がポアソン過程に従うとしている。
在庫のレベル\(s\)に応じて価格を変える戦略 \(\pi\) を考える。
例えば、在庫が10個以上あれば1000円で回収し、在庫が9個以下なら、1200円で回収するなどである。
この\(\pi\)のうち、一番コストが小さくなるものを最適化問題として解くことで求める。
戦略\(\pi\)のもとで、時刻tからTまでにかかる期待コストは以下の式で表される。
したがって、以下を満たす戦略\(\pi\)を求める。
詳細は省くが、ここから実際の設定により近づけた問題でも最適な解を導くことが可能である。
実験および結果
価格を固定した戦略と動的な戦略の比較実験を行った。
まず、価格を固定した時の最適な価格を求める。
これは上記の式において\(a(t)\)を固定すれば良いだけなので、解くことができる。
その価格でのコストを\(𝑔∗𝑠\)とする。これに対して、動的な戦略がどれだけコストを削減できたかという指標CR(Cost reduction)で評価を行った。
\(\lambda(𝑎)=𝑘𝑎\)として、\(k, a\), および、保管にかかるコスト\(h\)やLost Salesコスト\(𝑐𝑙\)などのパラメータに対し、1458通りの設定で実験を行った結果、以下のようになった。
| CR (%) | |
|---|---|
| Minimum | 0.36 |
| Maximum | 29.1 |
| Average | 10.16 |
コストは一定の価格よりも動的な価格を採用することで大幅に下げることが出来る
まとめ
調べた限りでは、機械学習によるダイナミックプライシングが適用されているのはまだ自動車などの一部の領域しかない。
中古品のダイナミックプライシングの難しさは価格を変更する要因が保存状態や経過年数など多数あることと在庫管理を考えないといけないことが原因である。
1つ目の価格の変更要因に関して、メルカリなどのフリーマーケットでは、汎用的なプライシングをするため、妥当な価格設定というのはなかなか難しいと思われるが、カメラなどの特定の分野を持つリユースショップの蓄積された知見を用いることでより良いダイナミックプライシングが可能になるのではないかと思う。
2つ目の在庫管理に関しては、Xiongら[6]のような研究はまだ少ない。需要予測に関する研究は盛んであるため、この二つを組み合わせた研究が進めば、中古品へのダイナミックプライシングの適用が進んでいくだろう。
参考文献
1,環境省,平成27年度使用済製品等のリユース促進事業研究会 リユース読本
http://www.env.go.jp/recycle/circul/reuse/confs/tokuhon_1.pdf
2, 2019年度「フリマアプリ利用者と非利用者の消費行動」に関する意識調査
https://about.mercari.com/press/news/article/20190425_consumersurvey/
3,月額1万円,「売れるクルマ」を事前に予測するAIシステム新発売!
http://www.recruit-mp.co.jp/news/pdf/20161101_01.pdf
4,Mercari Price Suggestion Challenge
https://www.kaggle.com/c/mercari-price-suggestion-challenge
5,Kaggleは凄かった! 更に簡単な出品を目指して商品の値段推定精度を改善中 – Mercari Engineering Blog
https://tech.mercari.com/entry/2018/11/14/172509
6,XIONG, Yu, et al. Dynamic pricing models for used products in remanufacturing with lost-sales and uncertain quality. International journal of production economics, 2014, 147: 678-688.
