スポーツチケット×ダイナミックプライシングの事例調査 - ダイナミックプライシングテクノロジー developers lab

Makoto Kirihata

コンテンツ

概要

需要と供給に合わせ、その時々で価格を変えて販売をするダイナミックプライシングが近年色々なスポーツで取り入れられている。

特にアメリカでは盛んで、NLBやNBA、NFLではほぼ全ての試合で導入されている。

日本では、プロ野球の一部のチーム、サッカーのJリーグで導入されてきている。

ダイナミックプライシングでは天候やイベント、過去の傾向などをAIによって分析し価格を決めると言われているが、実際にどういう原理が価格の決定に使われているかをきちんと説明している記事は少ない。

今回は以下の論文[1]で紹介されているアルゴリズムなどの手法について説明し、現状や今後の展望について考察していく。

モデルの式は載っていないものもあったので一部独自の解釈が含まれている。

[1] Xu, Joseph, Peter Fader, and Senthil Veeraraghavan. Evaluating the effectiveness of dynamic pricing strategies on mlb single-game ticket revenue. working paper, 2016.

野球での適用例

[1]は需要予測を活用したMLBチームのチケットにおけるダイナミックプライシングに関するワーキングペーパーである。

あるMLBチームが１シーズンの後半からダイナミックプライシングを取り入れており、その時期のチケット販売データを用いた実験を行う。

前半の価格が一定の期間で需要予測アルゴリズムを構築し、後半のデータでその需要予測モデルを用いたダイナミックプライシング戦略の評価を行っている。

実際に取り入れられていたダイナミックプライシング戦略の他に筆者らが提案した3種類のダイナミックプライシング戦略を価格を固定した場合と比較し評価を行う。

需要予測モデルの説明

需要 = game choice × ticket quantity dicision × seat section decision としてモデル化

すなわち、ある日$t$のゲーム$i$のセクション$s$のチケットの販売数 = ある日tにゲーム$i$のオーダー数 × あるオーダーにおけるチケットの購入数 × セクション$s$の席の購入選好

Game Demand Model(Game choice)

ある日$t$におけるゲーム$i$のオーダーの数$𝑛_{𝑖𝑡}$を負の二項分布回帰によりモデル化。

カウントデータでは一般にポアソン分布が使われるが、ポアソン分布では実際のデータの分散を上手く推定できないものがあり、そういう時には負の二項分布が使われる。

解釈がわかりやすいのでポアソン回帰について説明する。

ポアソン分布は以下の式で表され、$\lambda$の値によって図1のように分布の形が変化する。

\[ P(X = k) = \frac {\lambda^ke^{-\lambda}} {k!} \]

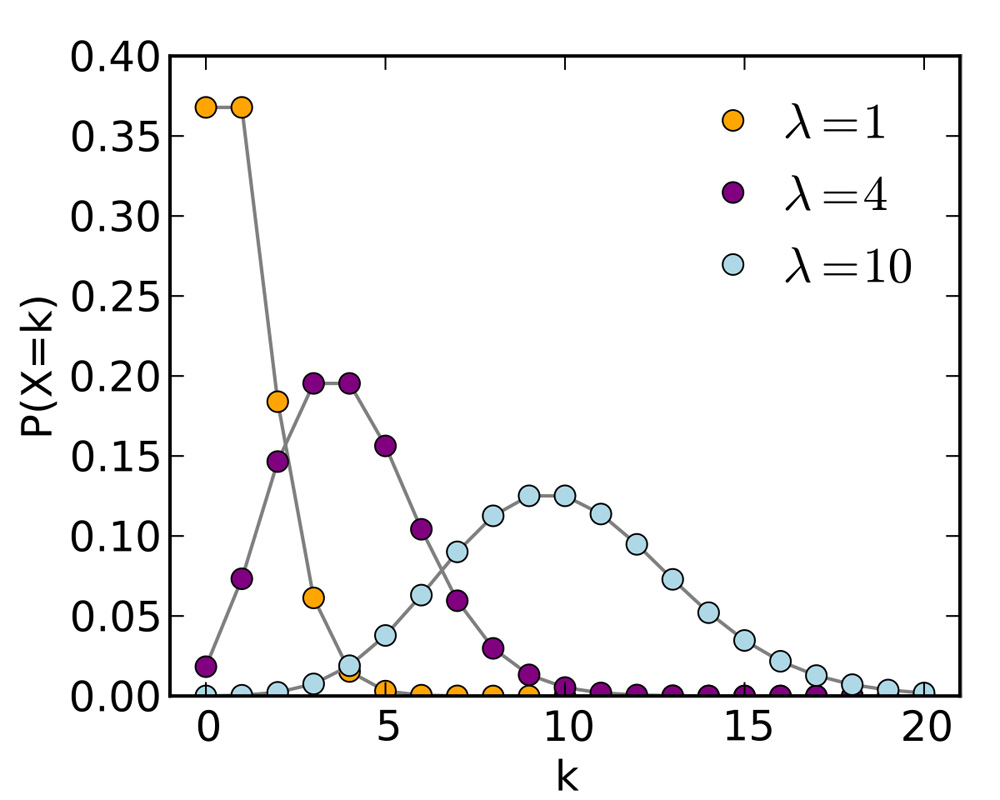
図1 引用 Wikipedia
https://ja.wikipedia.org/wiki/ポアソン分布

$P(X = k)$ は、ある時間内に平均で$\lambda$回発生する事象がちょうど$k$回発生する確率である。
今回でいうと、一日に平均で$\lambda$回のオーダーが発生する時、ちょうど$k$回オーダーが発生する確率。

ポアソン回帰の場合はこの$\lambda$が他の変数によって変化すると考える。

\[ \lambda = \beta o + \beta_1z_1 + \beta_2z_2 + \cdots + \beta_nz_n \]

各$zn$はゲームまで時間があるかないかやチームパフォーマンス、スタジアム、価格、残り席数などの影響がありそうな要因。
(ここでの価格と残り席数はスタジアム平均を使っており、ゲーム単位での違いしか考慮していない)

これを用いると、販売初日にゲーム$i$のオーダー数が10になる確率は0.3で、8になる確率は0.4などのようにオーダー数ごとに確率が求まる。

このモデル化したものと実際のデータで誤差が小さくなるように$\beta$の値を推測する。

Ticket Quantity Model

日付$t$のオーダー$j$における購入チケット数$xjt$を負の二項分布回帰によりモデル化。
Game Demand Modelと同じ変数を用いて平均的な値をモデル化し、パラメータ$\beta$を推定する。

ここまでの二つのモデルをかけ合わせるとある日$t$におけるゲーム$i$のチケット販売数の確率がわかる。

Seat selection model

ある価格設定で、残りチケット数がわかっている時、どのシートを選びやすいかを表現したモデル。

セクション$s$を選択する確率は価格$p_s$と占有率$o_s$が与えられているとすると以下のように表せる。

\[ P[Y_s = 1 ] = \frac {e^{\alpha_s} + \theta_1p_{s’} + \theta_2o_{s}} {\sum_{s’\in S}e^\alpha s’ + \theta_1p_{s’} + \theta_2o_{s’}} \]

$\alpha$が各セクション固有の選ばれやすさで、そこに価格と残りの席数が影響を与えて、現在の選ばれやすさを表現されている。

これもモデル化したものとデータで誤差が小さくなるようにパラメータを推定する。

評価の仕方

ここまでの3つのモデルと学習したパラメータを用いるとある日$t$におけるゲーム$i$のチケットのセクション$s$における販売数の確率が推定できる。

この販売数確率を用いて期待収益を計算し評価する。

全体の期待値は結構考えるのが難しいので、少し近似したもので考える。
収益を$R$、各セクションの残り席数を$u$とし、$p$は各座席セクションの価格のベクトル、$s$は各座席セクションの販売数のベクトルとすると

\[ R \tilde{ ( } t,u) = pE[s] + R \tilde{ ( }t – 1,x – E[s]) \]

$t$時点の収益=各セクションごとの価格$× t$時点の各セクションごとの販売数の期待値+1日前の収益

結構ナイーブな期待収益の計算方法だが、そこそこの精度で収益を計算できている。
ただし、最後のホームゲームだけ外れ値として除外している。

表1. Predicted Total Revenue vs Actual Total Revenue
	Total Revenue($K)	Error($K)	Error(%)
Observed	4,334	–	–
Predicted	4,132	-202	-4.66

収益の予測はあらゆる価格設定に対して計算することができるので、この期待収益の計算を様々な価格戦略に対して行い、ダイナミックプライシングの効果を検証する。

比較手法

文章でしか書いてくれていなかったので、少し違う部分があるかもしれない。

Baseline flat pricing
- 価格を変化させず、一定にしたもの
Actual Dynamic
- シーズン後半でチームが実際に行っていたダイナミックプライシング戦略
- 外部ベンダーの推薦により価格を変更
- 価格が前の日より下がることはない
Optimal variable pricing with look-ahead on team performance
- ゲームと席で価格を変動させるが、試合までの期間によっては変更しない
- ゲームごとの販売期間での予想収益を最大にする価格に設定する
  - 学習したモデルを使うとあらゆる価格設定に対して、セクションごとの販売数確率が出せるので、予想収益が最大になる価格を求めることが出来る
  - 販売開始時に最適な価格を決める必要があるので、パフォーマンスなどの要因は販売開始時の値に固定される
Monotone myopic dynamic pricing strategy
- ゲームと席と試合までの期間で価格を変更させる
- 1日の予想収益を最大にするように価格を決定
  - 直近までのデータを使って良い点が少し上と違う
- ただし、期間に関しては単調に値段が上がるという仮定を置く
Unrestricted myopic dynamic pricing
- 上のモデルを拡張して値段は上がっても下がっても良いとする
- ただし、事前に決められた上限下限がある

結果

表2. Optimal Flat Pricing Revenue and Optimal Dynamic Pricing Revenue
	Total Revenue($K)	Change($K)	Change(%)
Flat pricing	4,165	–	–
Actual Dynamic Pricing	4,132	-33	-0.79
Optimal Variable Pricing	4,729	564	13.54
Optimal Monotone Myopic Dynamic Pricing	4,310	145	3.48
Optimal Unrestricted Myopic Dynamic Pricing	4,760	595	14.29

既存のダイナミックプライシング戦略では収益が下がってしまっている。
これはチームのパフォーマンスが悪かったがそれを考慮できていなかったかららしい。
提案した3つの戦略では3番目が一番収益を改善した。

実験を通していくつかの発見があった。

販売期間の早い段階で価格を変更することにはほとんど価値がない
- 価格変更のほとんどは、需要が急激に増加し始める販売期間の終わり近くに発生する
- シートセクションに適切な初期価格を設定することには大きな価値がある
すべての座席セクションが同じような価格パスに従う必要があるわけではない
- 各座席セクションの適切な価格パスの種類は、ゲームまでの時間、チームのパフォーマンス、各セクションの残りの座席など、さまざまな要因によって異なる
単調増加のような価格の変動を制限するのはダイナミックプライシングの価値を下げる

現状と今後の展望

スポーツチケットにおけるダイナミックプライシングの手法としては、色々な要因を考慮した上で正確な需要予測モデルを構築し、戦略の評価をその需要予測により行うものだった。

他の論文でもこのような手法はよく使われており、この需要予測がどれだけ正確に行えるかが鍵となる。

しかし、価格の変更による影響はきちんと推測出来ていないと考えられる。
これは学習時の価格データが同じような値を取っていて、変動による影響を分析するのに十分な量がないからである。

したがって、価格弾力性の正体を解き明かす需要予測シミュレーションができるようになると、ダイナミックプライシング戦略の設定が容易になり、より利益を増大させることが出来るようになるだろう。

オリンピックを控えている今、スポーツへの注目が集まっているので、様々なスポーツでダイナミックプライシングの導入が進むのではないかと考えられる。

また、ダイナミックプライシングは人気のあるチームやスポーツだけに利益があると考えられがちだが、メインの部分は需要の分析であるので、コスト削減などにも応用することができる。

したがって、最近リーグが始まり収益を増加させたい日本のバスケットボールやバレーボール業界、ラグビーワールドカップ2019日本大会で盛り上がっているラグビー業界などでも活用されていくのではないかと考えられる。

参考文献

[1] Xu, Joseph, Peter Fader, and Senthil Veeraraghavan. Evaluating the effectiveness of dynamic pricing strategies on mlb single-game ticket revenue. working paper, 2016.

[2] 鈴木友也, 米スポーツ界に革命を起こしたダイナミックプライシング（上）革新的な値付け手法の誤解と真実, 2016/02/03, https://tech.nikkeibp.co.jp/dm/atcl/column/15/110200013/110900008/?P=1&ST=SIO-bus

この記事をシェアする