Miyamoto
1 はじめに
株式会社ダイナミックプライシングテクノロジーではダイナミックプライシングツールthroough(スルー)の新技術としてDQN(Deep Q Network)を導入しています。
そのため本記事では、DQN についての簡単な解説を行います。
▼throough(スルー)公式サイトURL
2 強化学習とは:DQN (Deep Q Network) 概説

強化学習とは、良い行動を選べるようにしていく人工知能・機械学習の一分野です。
一般的には、「実際に行動してみてその結果を見て行動を評価していく」という手法を、「強化学習」と呼ぶことが多いです。
2.1 notation
\(x\) がとりうる状態。\(a \)が行動です。いろんな \( x \) に対して、いい感じの \( a \) を選択したいというタスクです。時刻\(t \) での状態を \( x_t\)、行動を \( a_t \) と表記します。
方策関数\(\pi (a \mid x)\) というものを作ります。これは\(x\)を入れたら \( a \) が出てくるもので、多くの場合は確率的に \( a \) が出力されます。この \( \pi \) をいい感じの選択を選べるものにしていきたい。
ここで、「いい感じ」というものをどう定義するか。
それには「報酬」という概念を用います。 報酬は\(r\)であらわされ、\(x,a\)に対してランダムに決まるのですが、よい行動というのは「 \(r\)が大きくなる行動」とします。
少なくとも現状は、報酬を何にするかは人間が決めるしかなく、ここの選択によって、作られるAI の質は大幅に変化します。
いくら後述する累積報酬和最大化技術が優れていても、その土台となる報酬が良いものでなければどうにもなりません。
「報酬さえ最大化すれば、目的に合った良いAI が作れる」という状況を作るには、報酬の設計が重要となります。
ゲームAI のように勝ち負けといった非常にわかりやすい指標があれば楽なのですが、実社会での応用ではそうはいきません。
2.11 強化学習実応用で難しいポイント
いろいろな報酬を試すことができればよいですが、社会実装においてはそうはいかない場面が多いです。
例えば弊社の throough(スルー) のようなマーケティングAI では、AI による商品値付けを行うわけですが、実際に動かしてみなければならないという性質上、悪いAI は使っていただいたお客様に大きな損失を与えることになります。
さらに、これまでの売り上げをもとに行動を評価するため、一度試してからその報酬設計の評価を行うまでに時間がかかります。
他の社会実装分野にもタスク特有の難しさがあります。
例えばロボット分野での強化学習は、質の低いAI を用いた場合、高価な精密機械が損傷するリスクがあります。
物損や金銭的損失ならまだいい方で、自動運転分野だと人を撥ねてしまう可能性があります。質の低いAI がもたらす悪影響は計り知れません。
そのため、徹底した実情調査と、場合によっては機械学習の知見がなくとも、応用したい分野の専門家の協力なども経て、綿密に報酬設計を行っていく必要があります。
2.1.2 累積報酬和
報酬を大きくしたい、と聞いて、勘のいい方の一部は疑問に思ったかもしれません。
「今の報酬が少なくても、あとから良くなるような行動はいい行動なんじゃないの」と。
事実、経営などでも、一時的な損失を受け入れても、長い目で見れば得するような行動は良い行動ですよね。それを考慮するために、累積報酬和という概念を導入します。
(1)
\[ \sum_{t} \gamma^{t} r_{t} \]
\(\gamma\)は割引率と呼ばれ、0 以上で1より小さい定数です。
これは、お金で例えると「同じ金額をもらえるなら、来年もらうより今貰ったほうが嬉しい」というもので、ミクロ経済学や金融論でいう「割引現在価値」に該当します。
一期間ごとに、未来の利得の価値は \(\gamma\)倍されていきます。方策関数\(\pi\)を固定すると、\(x_0\)に対して \( a_0\)を決めて、 \( (x_0, a_0) \) によってランダムに\(x_1\)が決まって、それに対してまた\(\pi\)で\(a_1\)が決まり……、という形で無限に続けていくことができます。この\(\pi\)については、「\(\pi\)に対する累積報酬和の期待値」という数学的概念で評価します。
数式で書いてしまうと、
(2)
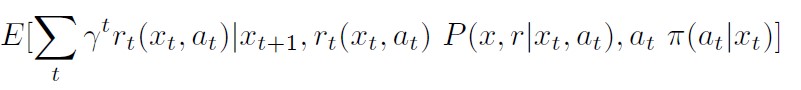
\(P(x,r \mid x_t,a_t)\)というのは、数学的には「遷移確率と即時報酬を表す確率測度」で、強化学習においては一般にはこれを推定する必要はありません。ただ、「裏で固定されている」と考えてください。
Q 関数
「累積期待報酬和で方策を評価するのは分かったけど、じゃあその未来の情報を必要とする累積期待報酬和はどうやって求めるの?」と思われた方もおられるかもしれません。これは、現在「\(Q\)関数」と呼ばれる手法を用いて行います。
\(Q\) 学習というのは、「状態行動価値関数」と呼ばれる関数です。その名の通り、\(x, a\)の組の価値を推定します。
方策オン型
それぞれの\(s, a\)に対して、 \(Q_{0}^{\pi} (s,a)\)という値を適当に決めてしまいます。そこから、次の更新式で値を更新していきます。
(3)
\[Q_{t+1}^{\pi}(s, a)=Q_{t}^{\pi}(s, a)+\alpha_{t}(s, a)\left[r_{t}(s, a)+Q_{t}^{\pi}\left(s^{\prime}, \pi\left(a | s^{\prime}\right)\right)-Q_{t}(s, a)\right]\]
ただし、\(s′\)は\(s,a\)に対する次の状態です。
これを無限に繰り返すと、一定の条件下で100%の確率で\(Q\)は正しい値に収束してくれます。
(4)
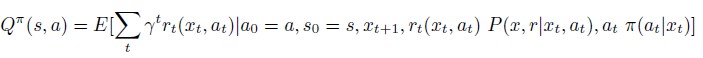
しかし、この方策を置くやり方には問題があります。すなわち「ほしいのは良い\(\pi\)なのに、その \(\pi\) の良さを評価するのに無限時間かかったらダメじゃん」ということです。
これを解決するために、一般には後述の方策オフ型と呼ばれる手法を使います。
2.2.2 方策オフ型
(5)
\begin{equation} Q_{t+1}(s, a)=Q_{t}(s, a)+\alpha_{t}(s, a)[r_{t}(s, a)+\max _{b} Q_{t}\left(s^{\prime}, b\right)-Q_{t}(s, a)] \end{equation}
これはgreedy(貪欲)法と呼ばれる手法です。これを無限回繰り返すことで、一定の条件下で最適な方策関数 \(\pi ^\ast\) に対応する\(Q\)関数(これを最適\(Q\)関数と呼び、\(Q^\ast\)と表記します)に100%収束します。\(^{*1}\)
最適 \(Q\) 関数には一つ大きなメリットがあります。それは「状態\(s\)に対して、最適 \(Q\) 関数の値が最大になる\(a\)を選ぶ」という戦略は、最適方策になるという点です。
方策オフ型で十分学習した \(Q\) 関数の各出力\(Q(s,a)\)は(これを\(s,a\)に対する\(Q\)値と呼びます)、\(Q^\ast(s,a)\)の推定値であり近似値であると考えられます。
つまり、これが最大になるような\(a\)を選ぶという行為は、最適方策\(\pi^\ast\)に従う行動をことに近いことが期待されます。
2.3 DQN (Deep Q Network) とは
ここまで、強化学習とは何かを説明してきました。しかし、まだ「じゃあやろう」と早速強化学習を実応用していくことはできません。
というのも、まだ「 \(Q\) 関数をどうやって実装するか」という大きな問題が残っています。DQNというのは、これをニューラルネットによって行う手法です。
DQN は”Deep Q Network”の略で、「ディーキューエヌ」と読みます。\(^{\ast 2}\)
一般的な手法では、\(a\)の取りうる種類は有限個とし、その数だけ出力層の次元を用意します。つまり、 \( a \) が全部で9種類あるなら、出力層のノード数は9とします。
\(s \) を入力し、9 次元のベクトルが出てくるニューラルネットを構成します。
次から一般的なDQNの学習における具体的な流れをお話しします。
2.3.1 その1:方策を決める
現在の状態\(s_t \) に対して、行動\(a_t \) を決定します。よくあるのは、「一定確率でランダムチョイス、残りは\(Q \) 値が最大になるものを」というやり方です。
ランダムチョイスは本当に適当に\(a_t \) を選ぶだけです。後者について説明します。
まず、DQNに\(s_t \) を入力し、それぞれの\(a \) に対する\(Q \) 値ベクトル\(\{ Q(s_t,a_1),……,Q(s_t,a_9)\} \)が出力されます。行動が10 種類あるなら、右端は当然\(Q(s_t,a_10)\)です。
この値の最大値をとるようなインデックス\(i\)に対して、\(a_i\)を今回の行動\(a_t\)とします。
2.3.2 その2:実際に行動して状態遷移と即時報酬を観測し、Q 値を更新する
実際に行動\(a_t\)を取ることで、即時報酬\(r_t(x_t, a_t),x_{t+1}\)が決定されます。この状態で(5)式によって \(Q\) 値を更新します。
するとまた、 \({Q(st_{+1}a_1),……,Q(s_{t+1},a_9)}\)というベクトルが出力されます。これを教師データとして、現在の \(Q\) 関数に\(s_{t+1}\)を入力した場合の出力を摺り合わせます。
この2段階を十分なステップ繰り返せば、より良い\(Q\)関数になっていくというわけです。
方策の選び方はSARASA法などほかの手法もあるのですが、この基礎編では割愛します。
スルーについて

3.1 スルーに実装されている3モデルについて
ここでは、現在スルーができる3つの最適化についてご紹介させていただきます。
\(^{\ast 1}\)これまで、これに対する厳密な証明はなく、あまりに穴の大きい証明を「理論的証明」と皆がありがたがって多数引用されている状況だったのですが、弊社研究チームが数学的に厳密かつ適用範囲を大きく広げた証明に成功しました。現在論文として発表する準備中です。
\(^{\ast 2}\) 字面を見れば、深層ニューラルネットしかDQN とは呼べないはずですが、三層でもDQN と呼ばれる場合が多いです。
3.1.1 利益最大化モデル
多数の商品の値段を調整するモデルです。強化学習技術により、登録した商品全体の合計利益を最大化します。
純粋に利益最大化のみを目指すので、粗利を上げる能力は一番高いモデルです。下記のような状況に当てはまらない場合は、こちらをおすすめします。
3.1.2 在庫処分モデル
在庫処分におすすめのモデルです。利益最大化効果は上記の利益最大化モデルほどはありませんが、食品のような厳格な期限がある場合にお勧めです。
3.1.3 ポイント最適化
ポイント還元を行う場合のコストを考慮した利益最大化をしたい場合におすすめです。
3.2 スルー独自の改良 ※専門的な話題です
ここからは発展編です。
\(Q\)関数から行動を選ぶ方法について。通常のQ Learning では上記の通り一定確率で \(Q\) 値が最大になる\(a\)を選択し、残りの場合はランダムに選ぶという方法がとられています。
しかしこれの問題点としては、1 番\(Q\)値が高い行動以外はすべて等価という点が挙げられます。この章では今後、行動は3 種類とします。
それぞれの\(Q\)値が[−10,4,3][−10,4,3]だとしたら、\(Q\)値が最大になる行動を選ぶなら行動2、そうでないなら3つの行動すべてから1/3 ずつの確率で選ばれます。
ここで重要なのが、行動3は、行動2ほどではないけどそれなりに良い行動であるにも関わらず、話にならない行動1と選ばれる確率が同じという点。
一方で、ベクトルを確率化するSARASA 法は、この問題点を解決してくれます。\(Q\)値を\(softmax\)関数にかけ、出てきた確率ベクトルを用いて乱数で行動を決めます。先ほどの例だと、\([6.078958339403138e – 07,0.7310581342225405, 0.2689412578816255] \)がソフトマックスの出力となり、行動2が73.1 %強、行動3が26.9 %弱の確率で選ばれることになります。
行動3と行動1に明確に差別化がされており、上記の問題点を解決したと言えるでしょう。
しかしSARASA 法には別の問題点があります。それは報酬のスケールの影響を受けるという点です。先述の通り、報酬の構成にはヒューリスティックな部分が大きく、定数倍の影響を受けるのは好ましくありません。報酬が何倍になろうと、同じ選び方をしてほしいのです。
しかし例えば上記のベクトルを2倍して\([-20, 8, 6]\)とした場合、ソフトマックスを通した確率ベクトルは\([6.090183410159188e – 13, 0.8807970779773459,0.11920292202204497]\)となり、確率が変わってしまっています。一方で通常の\(Q\)方策の場合は、定数倍の影響をうけません。
現在スルーに導入中の新技術は、この2手法両方の問題点を解決した手法となっております。論文にしていきたいと考えているため、まだ公開はできませんが、いち早く世界に先駆けてご利用いただけます。もちろん通常の学習方法でのご利用も可能です。
他にも巨大な市場をコンピューター上で再現し、そのシミュレーションによって学習を行う壮大な計画も立ち上がっております。続報をご期待ください。
