Miyamoto
1 はじめに
中心極限定理とは、確率論・統計学において非常に基礎的な概念であり、ほぼ全ての入門書に載っていると言っても過言ではないでしょう。
応用範囲も非常に広く、確率に関するたいていの分野で出てきます。
本記事では、その中心極限定理の基礎的な解説からはじめ、様々な応用について取り扱います。
2 中心極限定理とその発展
確率空間\((\Omega,\mathcal{F}, P)\)上で定義された独立な確率変数列\(\{X_{n}(\omega) \}_{n=1}^{N}\)を考えます。また、\(\mathcal{F}\)部分\(\sigma\)-加法族\(\mathcal{G}_N\)を考えて、これを「使える情報」とします。
2.1 推定量と分布収束、情報量の基礎
確率変数の収束と一口に言ってもたくさんの種類があり、必要条件十分条件の関係の把握が重要です。
その中で、今回は推定量に関する説明を行います。
2.1.1 推定量
今回、推定したい値\(\theta \in \mathbb{R}^{d}\)は定数と仮定。 \( ^{ \ast 1}\)これに対する\(\mathcal{G}-\)可測な予測値\(\hat{\theta}\)を「推定量」と呼びます。データから構成する値で、データは\( \mathcal{G} \)-可測な確率変数であるため、推定量も確率変数というわけです。
2.1.2 不偏推定量と一致推定量
\(\hat{\theta}\)は可測であればなんでも推定量と言い張れますが、もちろんその中での優劣は存在します。
定義1 不偏推定量
期待値は正しい値であってほしい、というのは当然のお気持ちでしょう。
(1)
\[\theta^{*}=E[\hat{\theta}]\]
が成り立つとき、\(\hat{\theta}\)を「不偏推定量」と呼びます。
定義2 一致推定量
データ数を無限に増やしても、きっちり正しい値に収束してくれはしない推定量はいいものであるとは言い難いです。
\(N\)個のデータから作られる推定量 \(\hat{\theta}_N\) に対して、 \(^{\ast 2}\)
(2)
\[\hat{\theta}_N \to \theta ^{\ast}\]
が成り立つとき、\(\hat{\theta}\)を「一致推定量」と言います。
収束が後述の概収束の場合これを「強一致推定量」、確率収束の場合これを「弱一致推定量」と言います。強一致、 弱一致と書かれておらず、単に一致としか書かれていない場合、ほとんどの文献においてこれは弱一致を指しています。
\(^{\ast 1}\)ベイズ推定では、ここを確率変数と考えて、その分布の推定を行います。本当に定数なのかは考慮しません。
\(^{\ast 2}\)適宜対応する\(\sigma\)加法族\(\mathcal{G}_N\)を考えます。
2.1.3 確率変数列の収束
確率変数列\(\{X_{n}\}_{n}\)の確率変数\(X\)への収束には、様々な種類があります。
定義3 概収束
(3)
\[\left.P\left(\omega | X_{n}(\omega) \rightarrow X(\omega)\right)=1\right)\]
が成り立つとき、この収束を「概収束」もしくは「\(\Omega\)上確率\(1\)で収束する」と言います。\(^{\ast 3}\)
\(^{\ast 3}\)一般の可測関数に対しては、「ほとんどいたるところ収束する」とも言います。
定義4 確率収束
任意の\(\epsilon , \delta > 0 \)に対して、ある\(N _\delta \)が存在し、 \(n > N _\delta \) となる任意の\(n\)に対して
(4)
\[P\left(\omega | | X_{n}-X |<\epsilon\right)<\delta\]
が成り立つとき、この収束を確率収束と言います。
定義5 法則収束
\(X_n\)の分布関数を\(F_n(x)\)とし、\(X\)の分布関数を\(F(x)\) とします。
(5)
\[F_n(x) \to F(x) \]
が\(F\)の任意の連続点に対して成り立つとき、「法則収束」といいます。
また、これと同値な定義として、任意の連続関数\(f\)に対して
(6)
\[E\left[f\left(X_{n}\right)\right] \rightarrow E[f(X)]\]
が成り立つことを法則収束の定義としてもかまいません。上のほうが直感的で理解がしやすいですが、実用ではなんだかんだ下のほうが使いやすい。
余談ですが、\(E[f(X)]\) のことを、対応する測度を用いて\(\pi _X(f)\)と略記することもあります。SDEの統計なんかではよく出てくる。
法則収束は別名分布収束です。上の定義そのままの名前ですね。
2.2 中心極限定理
中心極限定理のうち、最も基礎的なものを次に述べます。簡単な本とかに載ってるのは基本的にこれ。
定理1 中心極限定理
確率変数列\(\{X_n\}n\)は独立同分布に従う確率変数列で、\(E \left[X_{1}\right]=\mu, V\left[X_{1}^{2}\right]=\sigma^{2}\)であるとする。このとき、\(S_{n}:=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)\)と置くと、
(7)
\[\sqrt{n} S_{n} \rightarrow N\left(0, \sigma^{2}\right)\]
ただしこの収束は法則収束です。
2.3 中心極限定理の改良
中心極限定理には様々な改良版があり、そこで重要になってくるのが、このLindeberg 条件です。
定義6 Lindeberg 条件
確率変数列\(\{X_n \}_n\)はすべて互いに独立かつ\(L ^2\)で、対応する測度を\(m_i\)とする。
\(E\left[X_{k}\right]=\mu_{k}, V\left[X_{k}\right]=\sigma_{k}^{2}, t_{n}:= \sum_{i=1}^{n} \mu_{i}, s_{n}^{2}:=\sum_{i=1}^{n} \sigma_{k}^{2}\)とする。任意の\(\epsilon > 0\)に対して
(8)
\[\frac{1}{s_{n}^{2}} \sum_{i=1}^{n} \int_{\left|x-\mu_{i}\right|>\epsilon s_{n}}\left(x-\mu_{i}\right) d m_{i}(x) \rightarrow 0\]
これが成り立つとき、「Lindeberg 条件を満たす」と言う。
定理2 Lindeberg の中心極限定理
Lindeberg 条件を満たすとき、
(9)
\[\frac{S_{n}-t_{n}}{s_{n}} \rightarrow N(0,1)\]
法則収束の意味で成り立ちます。
次の定理が、Lindeberg-Feller の中心極限定理です。おそらく一番使いやすいでしょう。
定理3 Lindeberg-Feller の中心極限定理
任意の\(\epsilon > 0\)に対して
(10)
\[ \lim _{n \rightarrow \infty} \max _{1 \leq k \leq n} P\left(\left|X_{k}-\mu_{k}\right|>\epsilon s_{n}\right)=0 \]
が満たされるとき、これはLindeberg 条件を満たす。つまり\(\frac{S_{n}-t_{n}}{s_{n}} \rightarrow N(0,1)\)が分布収束の意味で成り立つ。
Lindeberg 条件は十分条件ですが、\(max _i X_i\)の変動が分散の和の増大と比べて極めて小さい場合\(^{\ast 4}\)は必要十分条件となります。
最後に、発展編として離散時間確率過程に関する定理を紹介します。
\(^{\ast 4}\) \(max _{k < n} \frac{\sigma_{k}^{2}}{s_{n}} \rightarrow 0\)が成り立つ場合。
定理4 マルチンゲール中心極限定理
ここまで紹介した定理はどれも独立性を仮定していましたが、この条件を大幅に緩めることができます。 増大情報系\(\mathcal{F}{0} \subset \mathcal{F}{1}, \ldots \ldots \subset\)を考えます。
確率過程\(\xi _i\)がマルチンゲール差分列であるとは、 \(\xi _n\)が\(\mathcal{F}_n\) 可測で、\(E\left[\xi_{i} | \mathcal{F}_{n-1}\right]=0\)がなりたつことを言います。また、ある\( \xi > 0\)が存在して
(11)
\[\sum_{i=1}^{n} E\left[\left|\xi_{i}\right|^{2+\delta} | \mathcal{F}_{i-1}\right] \rightarrow 0\]
が確率収束の意味で成り立ち、そのうえで
(12)
\[\sum_{i=1}^{n} E\left[\left|\xi_{i}\right|^{2+\delta} | \mathcal{F}_{i-1}\right] \rightarrow C(定数)\]
であるとき、\(\sum_{i=1}^{n} \xi_{i} \)は\(N(0, C)\)に分布収束する。
2.4 一般化中心極限定理
ここまで分散は有限であるとしていましたが、分散が無限の場合にも中心極限定理が成り立ちます。
定義7 安定分布
\(0<\alpha \leq 2,-1 \leq \beta \leq 1, \gamma>0\)は定数と定義する。
次のような特性関数で表現できる確率分布を安定分布と言う。
(13)
\[\phi(z)=\exp \left[i \delta z-\gamma|z|^{\alpha}{\{1+i \beta \operatorname{sgn}(z) \omega(z, \alpha)\}}\right]\]
(14)
\[\omega(z, \alpha):=\begin{cases}\tan \frac{\pi \alpha} 2 & (\alpha \neq 1)\\\frac 2{\pi} \log |z| & (\alpha=1)\end{cases}\]
これは様々な分布の一般化で
- \(\alpha = 2 \) のとき、平均\(\delta\)で分散\(2 \gamma \)の正規分布になる
- \( \alpha = 1, \beta = 0 \)のとき、中央値 \(\delta\) で尺度母数\(\gamma\)のコーシー分布となる
- \(\alpha = 2 \) でないとき分散を持たない(二次モーメントが無限大になる)
といった特徴を持ちます。\( \alpha \)を特性指数と呼びます。
定理5 一般化中心極限定理[1]
確率変数列\(\{X_n\}_n\)の密度関数が、次のファットテール分布に従うとする。
(15)
\[\phi(z)=\mathcal{exp} \left[i \delta z-\gamma|z|^{\alpha}\{1+i \beta \operatorname{ \mathcal{sgn}}(z) \omega(z, \alpha)\}\right]\]
(16)
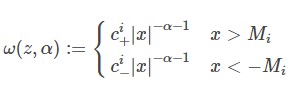
この時、\(S_{n}:=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu_{i}\right)\)とおくと、これは特性指数\(\alpha\)の安定分布に分布収束する。 \(\alpha = 2 \) のときこれは普通の中心極限定理とほぼ同じです。
3 中心極限定理の使い道
中心極限定理は確率が絡む場所のほとんどで使われているのですが、強化学習に近いところで、かつ直接的な事例のうち極一部を紹介していきます。
3.1 経験過程
確率変数の分布を推定するにあたって、一番手っ取り早いのは経験分布をみることです。
独立同分布な\(L^2\)確率変数列\(\{X_{n}\}_{n=1}^{\infty}\)を考えます。
データが\(n\)個の時の分布関数の予測値\(F_n\)を
(17)
\[F_{n}(x):=\frac{1}{n} \sum_{i=1}^{n} 1_{\left.X_{i} \in(-\infty, x]\right)}\]
とします。めちゃくちゃ「そのまんま」感が漂う雑な定義ですが、なんとこれでもデータが十分あればいい感じに分布を推測できます。
定理6 経験分布の性質
真の分布関数を\(F(x)\)と置くと、
(18)
\[\underset{x}{\mathrm{SUP}} \left|F_{n}(x)-F(x)\right| \rightarrow 0 \quad \text { a.e. } (強一致性) \]
(19)
\[E\left[F_{n}(x)\right]=F(x) (不偏性)\]
(20)
\[\sqrt{n}\left(F_{n}(x)-F(x)\right) \rightarrow^{L} N(0, F(x)(1-F(x))) (漸近正規性)\]
が任意の\(x\)で成り立ちます。強一致性については一様収束の意味で成り立ちます。\(^{\ast 5}\)
漸近正規性は中心極限定理から示されます。
\(^{\ast 5}\) ちなみに最後の漸近正規性による分布収束先はbrownian Bridge と言います。
3.2 最尤推定
漸近正規性は、通常の正規分布への確率収束よりも多くの情報を含んでいます。
(21)
\[\sqrt{n}\left(\hat{\theta}-\theta^{*}\right) \rightarrow^{L} N\left(0, \sigma^{2}\right)\]
が成り立つとき、これを漸近正規推定量と言います。
この魅力は、なんといっても\(\sigma\)が小さいほど早く収束するという、収束の速さの評価ができるという点です。
最尤推定は漸近正規性を持ちます。 \(\sigma\) の下限はクラメールラオの不等式によりフィッシャー情報量の逆数となります。\(^{\ast 6}\)
3.3 SDE の統計
確率微分方程式(SDE)における統計理論でも、中心極限定理は当然のように登場し続けます。\(^{\ast 7}\)
今回は、その非常に簡単な例として、累積ボラティリティの推定を行います。
\(t \in [0,1]\)上で次の確率微分方程式を考えます。
(22)
\[d X_{t}=\mu_{t} d t+\sigma_{t} d B_{t}\]
ただし、\(\mu _t, \sigma _t\)は適合な左連続右極限であるとします。
ここで、累積ボラティリティIVとその推定量RV を構成します。
(23)
\[I V:=\int_{0}^{1} \sigma_{s}^{2} d s\]
(24)
\[R V_{n}:=\sum_{i=1}^{n-1}\left(\Delta X_{t_{i}}\right)^{2}\]
ただし、\(t_{i}=i / n, \Delta X_{t_{i}}:=X_{t_{i+1}}-X_{t_{i}}\)とします。
IV の期待値は、伊藤積分の等長性からSDE の第二項の二次モーメントと一致します。
ここで、\(RV_n\)には一定の条件下で安定収束という別の意味での漸近正規性が成り立ちます。すなわち、
(25)
\[\sqrt{n}\left(R V_{n}-I V\right) \rightarrow^{L} N(0, \sqrt{\left.2 \int_{0}^{1} \sigma_{s}^{4} d s\right)}\]
です。さらに弱一致推定量となることが示されています。
\(^{\ast 6}\) 雑に言えば、情報量多いほどそこから作られた推定量は安定しており質が高いぞ、という当たり前の帰結。逆に言えば、情報から得られるもの以上によい推定量などないというこれまた当然の考え。
\(^{\ast 7}\) そもそもブラウン運動の定義自体が汎関数中心極限定理で成されたりします。
3.4 SDE の数値解析
前項も数値解析的なお話になってしまいましたが、ここでも数値解析の話をします。
次のような1 次元の確率微分方程式を考えます。
(26)
\[X_0 = x\]
(27)
\[dX_t := b(t,X_t)dt + a(t,X_t)dB_t\]
それに対してオイラー丸山スキームでの近似\(t_k := k/n\)とすると
(28)
\[X_{t_{k+1}}^{n}=X_{t_{k}}+\frac{1}{n} b\left(t_{k}, X_{t_{k}}\right)+a\left(t, X_{t_{k}}\right) \Delta B_{t_{k}}\]
と置けます。
この離散近似の挙動を考えたいのですが、これは中心極限定理から\(Z\)を標準正規分布に従う確率変数として
(29)
\[\left|X_{1}^{n}\right|^{2} \sim|x|^{2}\left(1+\sqrt{\frac{2}{n}}+O\left(\frac{1}{n}\right)\right)\]
が成り立つことが広く知られています。
4 さいごに
本記事では中心極限定理の基礎解説と、その応用についての導入に触れました。強化学習でも、分布型強化学習といった重要なテーマでも今後必ず登場するであろうことが推測されます。
次回、連続時間の強化学習に関する記事を出します。お楽しみに。
参考文献
[1] Voit, Johannes . The Statistical Mechanics of Financial Markets. Springer-Verlag.
[2] 楠岡成雄, 数理ファイナンスに現れる数値計算の確率解析手法
